sinθ = Opposite Hypotenuse Now if we increase the magnitude of θ slowly then the magnitude of opposite will slowly go to increase and the magnitude of adjacent will go to decrease When θ becomes equal to π 2 then adjacent will vanish and opposite will coincide with the hypotenuse This means when θ = π 2 then "opposite"="hypotenuse"#1 Use the given function value and the trigonometric identities to find the exact value of each indicated trigonometric function 2 Construct an appropriate triangle to complete the table (0° ≤ θ ≤ 90°, 0 ≤ θ ≤ π /2) 3 Construct an appropriate triangle to find the missing values 4Extended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, music
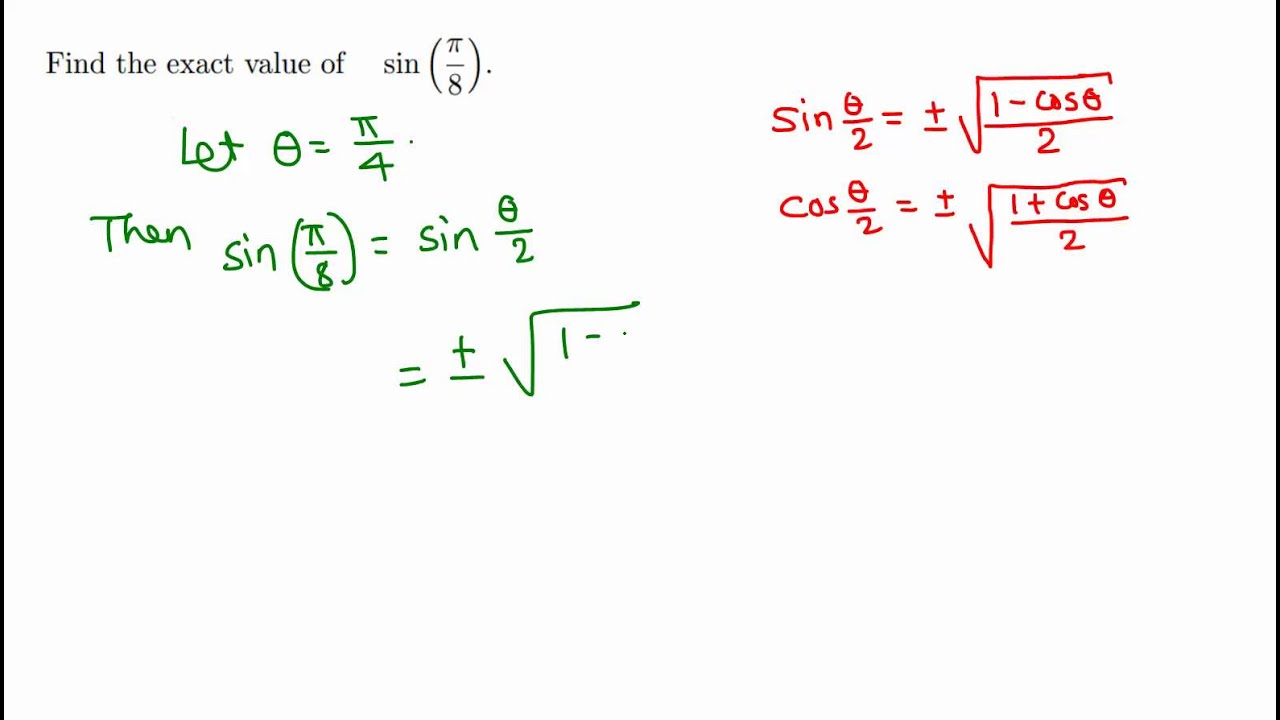
Trigonometry Exact Value Of Sin Pi 8 Sin 22 5 Youtube
Sin π/2 value
Sin π/2 value-$$\begin{align}\sin\left(2n1)\frac\pi2\right&= sin(nππ/2)\\ &= \sin(n\pi) \sin \left(\frac\pi2\right)\\ &= 0 1The trigonometric R method is a method of rewriting a weighted sum of sines and cosines as a single instance of sine (or cosine) This allows for easier analysis in many cases, as a single instance of a basic trigonometric function is often easier to work with than multiple are The R method is most often used to find the extrema (maximum and minimum) of combinations of trigonometric




Cos Pi 2
The value of ∫_(π/2)^(π/2)dx/(xsinx 4) where t denotes the greatest integer less than or equal to t, is (a) 1/12(7π5) (b) 3/10(4π3)(c) 1/12(7π5Firstly, when people are first learning trigonometry, things are much easier to follow if they use DEGREES!Sin(3π/2), sin(270°)1 cos(π/6), cos(30°)
Sine calculator online sin(x) calculator This website uses cookies to improve your experience, analyze traffic and display ads Thus arcsinx arccosx = π 2 Draw a right triangle whose hypotenuse has length 1 and say the side of it opposite one of the angles, θ has length x Then the side of it adjacent to the other acute angle is that same side of length x The other acute angle is π / 2 − θ So θ = sin − 1x and π / 2 − θ = cos − 1x The value of ∫(π/2 → π/2) sin 2 x/(12 x)dx is (1) π/8 (2) π/2 (3) 4π (4) π/4 jee;
Sin π 2 −α =cosα cos π 2 −α =sinα We have already proven all these identities, except the cofunction identities We have already mentioned them when we studied transformations of the graphs of sine and cosine There is a nice way to prove them using a triangle Consider the triangle below In this triangle, we have sinα = a c cosβThe sin value when angle of a right triangle equals to 90 ° is called sine of angle 90 degrees In mathematics, it is written as sin ( 90 °) according to sexagesimal system sin ( 90 °) = 1 The value of sin of 90 degrees is 1 exactly and it is often called as trigonometric function (or ratio) for standard angle generally The direction #theta= (3pi)/2 separates 3rd and 4th quadrants Sine is negative in these quadrants sin(π θ) = sin(2π− θ) = − sinθ sin(3π 2) =




Find The Value Of The Following A Sin Pi 6 B Cos Pi 4 C Tan Pi 3 D Cos Pi 2 E Cot 3pi 4 F Sin 5pi 6 G Sin Pi H Cos Pi I Sin Pi 2 J Sin 3pi 2 K Cos 3pi 2




Ex 2 2 Find Sin Pi 3 Sin 1 1 2 Class 12 Ncert
Question Find the absolute maximum and absolute minimum values of f on the given interval f(t) = 2 cos t sin 2t, 0, π/2 absolute minimum value and absolute maximumm valueShare It On Facebook Twitter Email 1 Answer 1 vote answered by rubby (5k points) selected by Vikash Kumar Best answer Ans 4The sine calculator allows through the sin function to calculate online the sine sine of an angle in radians, you must first select the desired unit by clicking on the options button calculation module After that, you can start your calculations To calculate sine online of π 6, enter sin ( π 6), after calculation, the result 1 2 is returned




If Sin 1 X 5 Cose C 1 5 4 Pi 2 Then The Value Of X Is 1 1 2 3 3 4 4 5




Find The Principal Value Of Tan 1 Sin Pi 2
Free math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutorThe most that the numerator can be is equal to the denominator A sine or cosine can never be greater than 1, so a value of 171 must be wrong Wanted sine, cosine, or tangent, of whole angle (A B) Finding sin(A B) The easiest way to find sin(AIf Sin 1 1 X 2sin 1 X Pi 2 Then X Is Equal To If sin 1 (1 x) 2sin 1 x = π / 2, then x is equal to 1) 0, – (1/2) 2) 0, 1/2




If Sin X 5 3 And 0 Lt X Lt P 2 Find The Value Of Sin 2x Cos 2x Tan 2x Brainly In
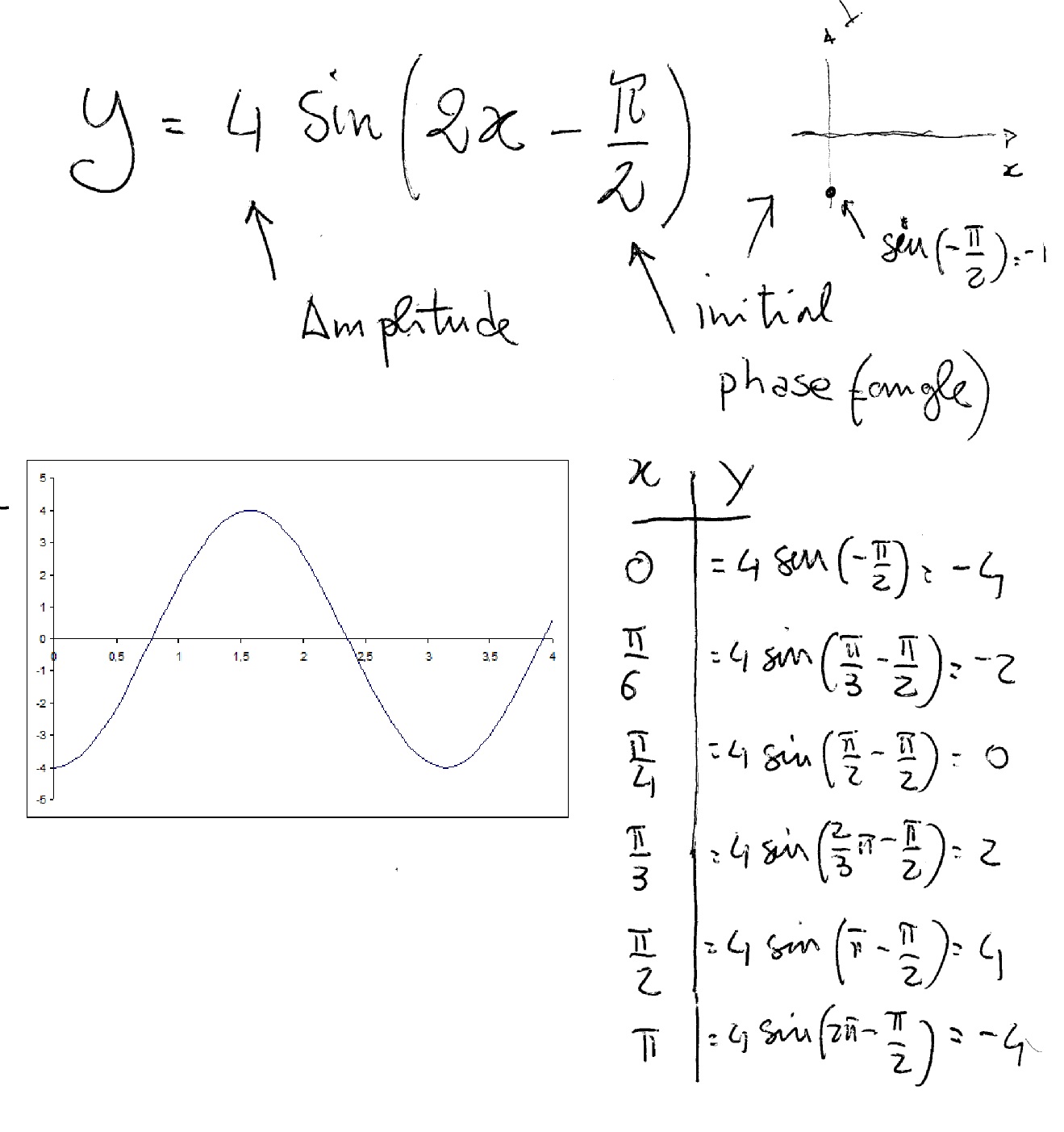



How Do You Graph Y 4sin 2x Pi 2 Socratic
If the angle is multiple of π/2, ie π/2, 3π/2, 5π/2, then sin becomes cos cos becomes sin If the angle is multiple of π, ie π, 2π, 3π, then sin remains sin cos remains sin 2The sign depends on the quadrant angle is in sin (π/2 – x) Since it is π/2, sin will become cos Here x is an acute angle So, π/2 – x = 90 – x is anTrigonometric identities are equations involving the trigonometric functions that are true for every value of the variables involved Some like the following sin 2 ( x ) cos 2 ( x ) = 1 1 tan 2 ( π 2 − x ) = sec ( x )Sin 90° = 1 The most common trigonometric sine functions are Sin 90 degree plus theta Sin 90 degree minus theta Some other trigonometric sine identities are as follows Sin 2x = 2 sin x cos x In the same way, we can derive other values of sin angles like 0°,
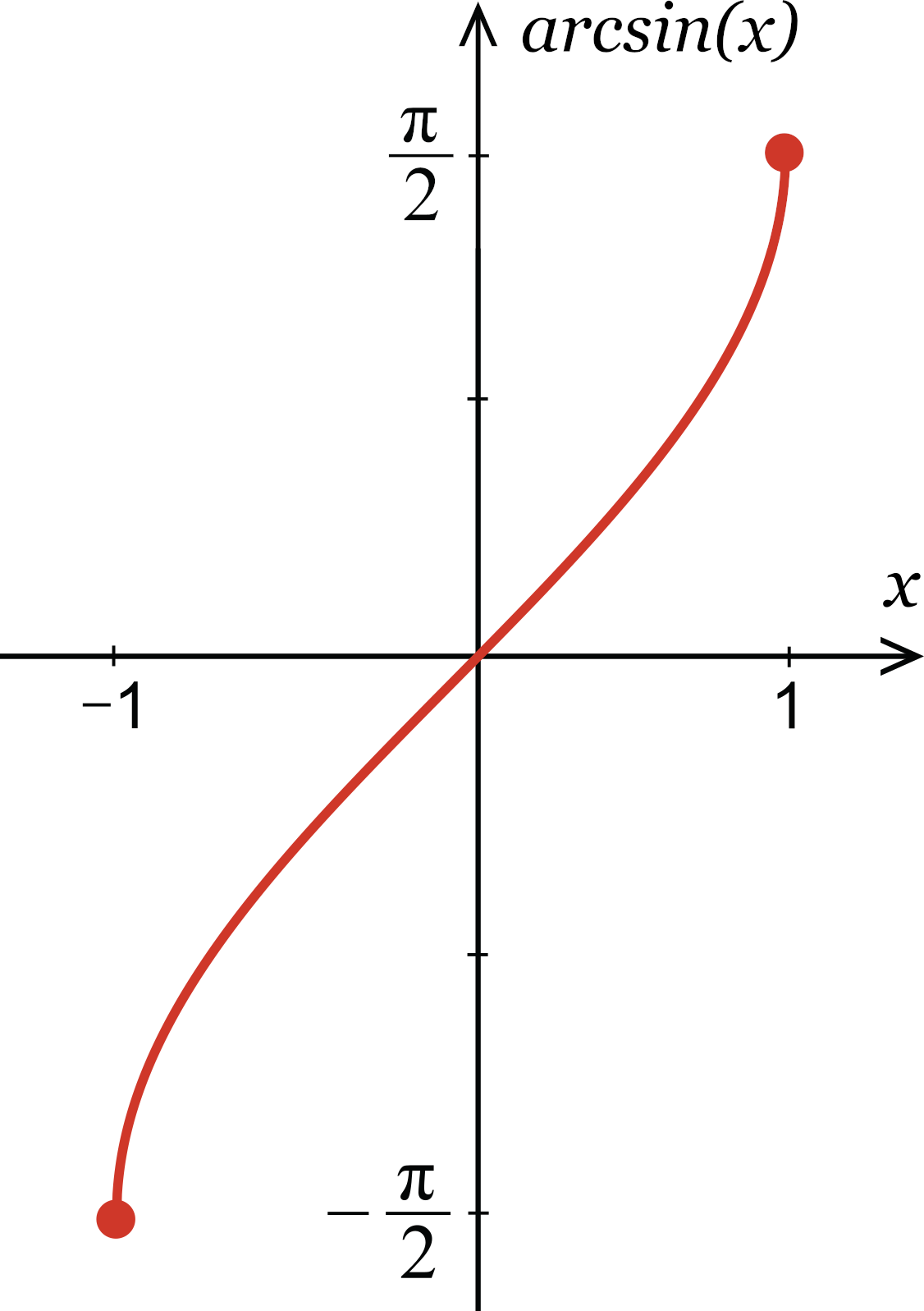



Inverse Sine Calculator Calculate Arcsin X Inch Calculator




Solution What Is The Integral Of Sin 5 X Cos 3 Xdx
The value of sin θcos θ will be greatest when θ=30∘ θ=45∘ θ=60∘ θ=90∘ Let fx=sin θcos θ=√2sinθπ4But−1≤sinθπ2≤1⇒−√2≤√2sinθπ4≤√2Hence the maximum value oExtended Keyboard Examples Upload Random Compute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, history, geography, engineering, mathematics, linguistics, sports, finance, musicMaximum points (π/2 2kπ, 1), where k is an integer • Minimum points (3π/2 2kπ, 1), where k is an integer • Symmetry since sin (–x) = –sin (x) then sin(x) is an odd function and its graph is symmetric with respect to the origin (0, 0) • Intervals of increase/decrease over one period and from 0 to 2π, sin (x) is



What Is The Value Of Sin Pi 6 Socratic




2 39 Find The Value Of T 0 P Frac Cos Gauthmath
Sin(t) = 1/2 t = { pi/6, 5pi/6 } but 5pi/6 is outside of the interval, so reject it sin(t) 1 = 0 sin(t) = 1 t = {3pi/2} but reject this because it's outside of our interval Therefore, critical numbers are only t = pi/6 Plug this value into the function f(pi/6) = 2cos(pi/6) sin(2*pi/6) f(pi/6) = 2sqrt(3)/2 sin(pi/3) f(pi/6) = sqrt(3Remove full rotations of 2π 2 π until the angle is between 0 0 and 2π 2 π sin(π 2) sin (π 2) The exact value of sin(π 2) sin (π 2) is 1 1 1 1 1 Answer 1 vote answered by Naaz (4k points) selected by Eihaa Best answer Let sin–1 (1 √2 1 2) = x ∴ sin x = 1 √2 1 2 ∴ sin x = sin π 4 π 4 The principal value branch of sin–1 x is − π 2, − π 2, π 2 π 2 and − π 2 − π 2 ≤ − π 4 − π 4 ≤ π 2 π 2
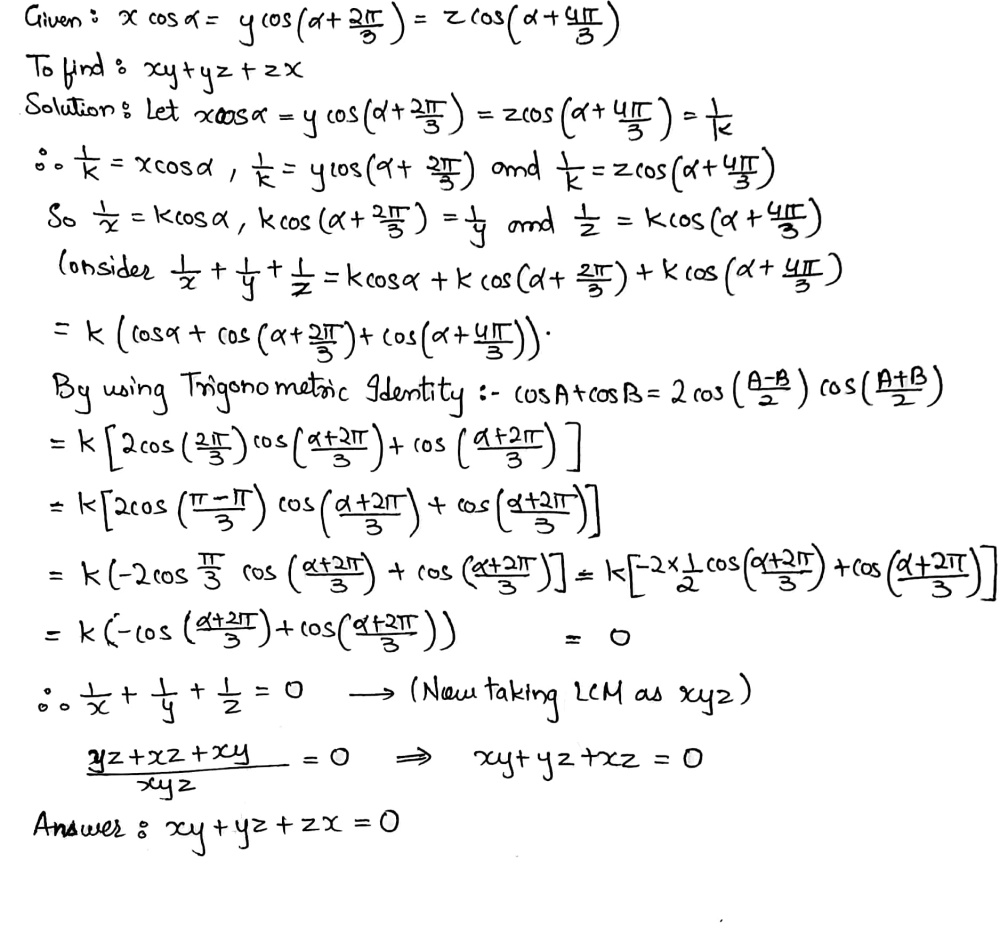



If Scos Alpha Ycos Text 61 Alpha Frac 2pi 3 Zcos Left Alpha Frac 4pi 3right Then Find The Value Of Xy Yz Zx Snapsolve




Verify Lagranges S Mean Value Theorem For The Following Function F X Sin X On Left Dfrac Pi 2 Dfrac 5pi 2 Right
The Value of Tan X Sin ( π 2 X ) Cos ( π 2 − X ) CBSE CBSE (Science) Class 11 Textbook Solutions Important Solutions 9 Question Bank Solutions 9935 Concept Notes & Videos 580 Syllabus Advertisement Remove all ads The Value of Tan X Sin ( π 2 X ) Cos ( π 2 − X )Write the Principal Value of Cos − 1 ( Cos 2 π 3 ) Sin − 1 ( Sin 2 π 3 ) CBSE CBSE (Arts) Class 12 Question Papers 17 Textbook Solutions Important Solutions 24 Question Bank Solutions Concept Notes & Videos 531 Time Tables 18 SyllabusY = sin (x π) In the above graph of y = sin (x π), the graph has been shifted by a unit of π to the left In fact, a positive phase shift c actually indicates a shift to the left Let's look at some more examples y = sin (x 1) The sine curve shifted one unit to the left y = sin (x π/2) The curve shifted π/2 units to the left




Simplify Sin P 6 I Cos P 6 18 Brainly In
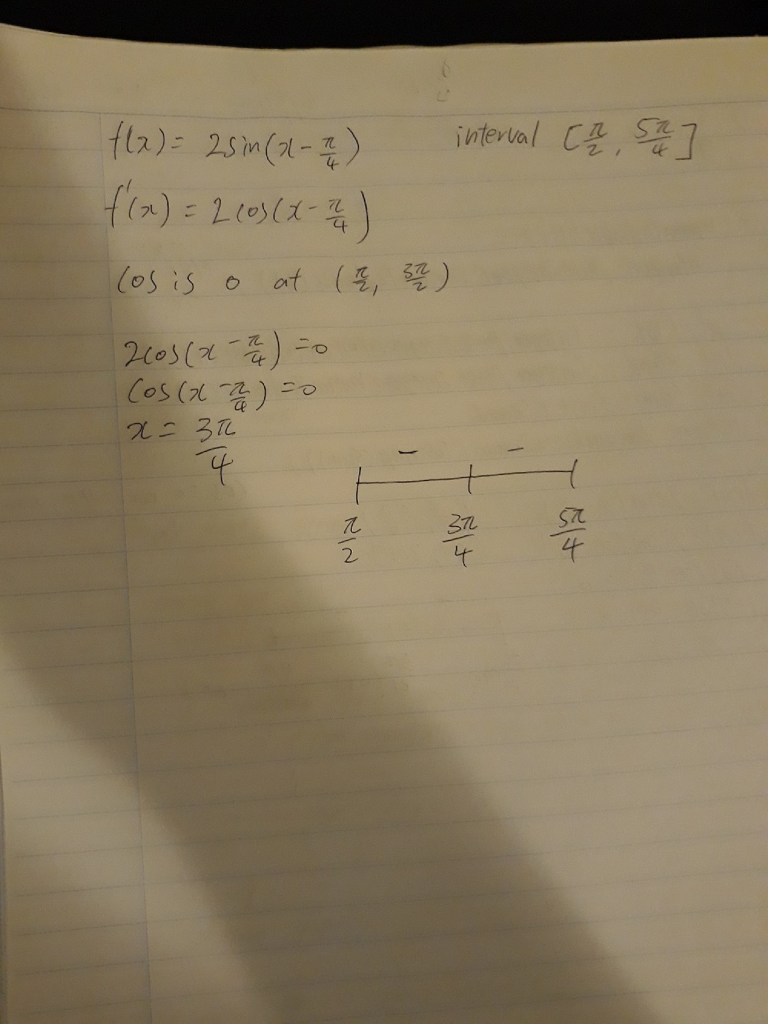



F X 2 Sin X P 4 On The Interval P 2 5p Chegg Com
I hope you know that π/2 rads = 90 degrees This is the graph of y = sin(x) from x = 360 to 7 degrees Now if we consider sin(n × 90) w We say the cosine curve is a sine curve which is shifted to the left by `π/2\ (= 157 = 90^@)` The value of the cosine function is positive in the first and fourth quadrants (remember, for this diagram we are measuring the angle from the vertical axis),The value of sin (π 2) is fairly well known to be 1 sin − 1 (1) Since the inverse sin function doesn't know where that 1 came from, it has to assume it came from angles between − π 2 and π 2 That means it will evaluate that inverse sine to π 2 This same reasoning can be used for a value of 10 sin (10) ≈ − 0
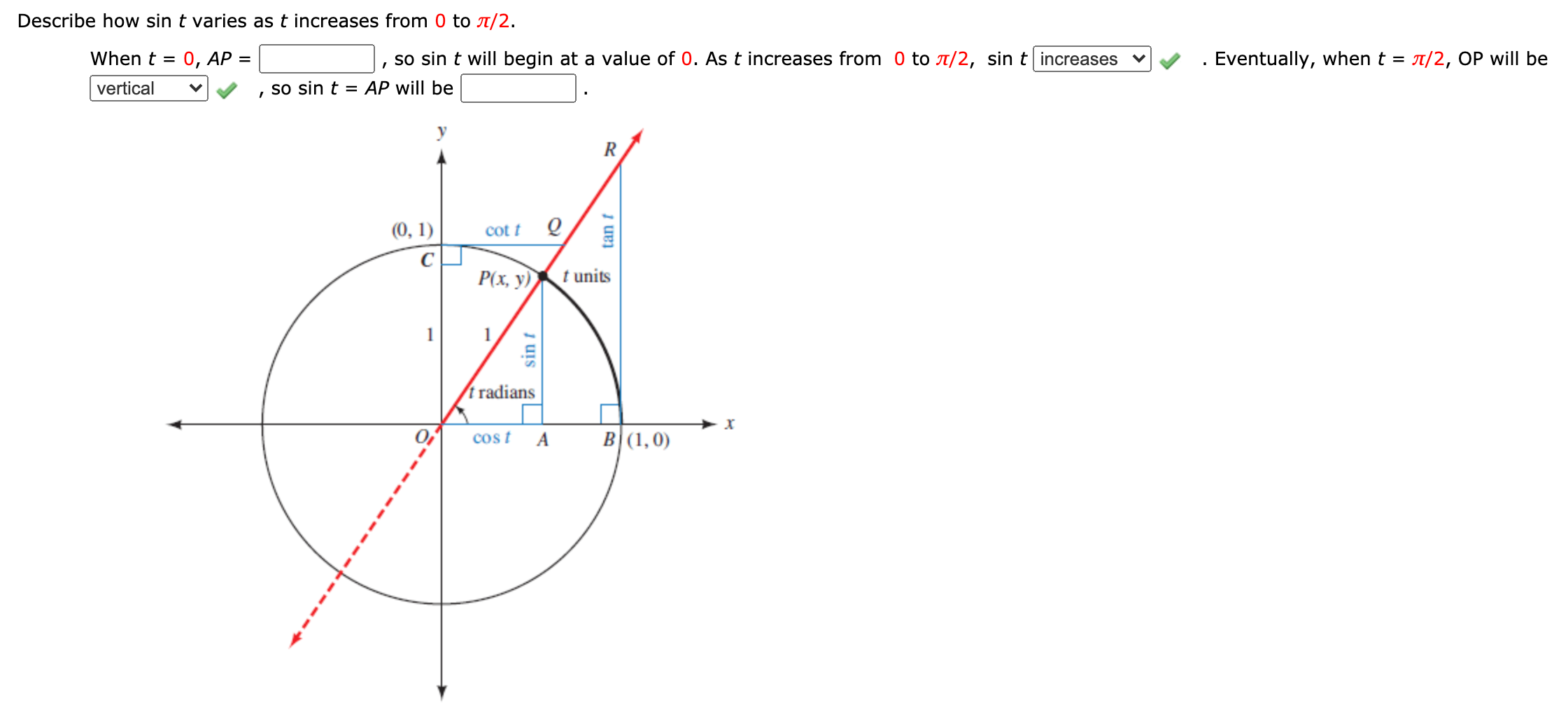



Answered Describe How Sin T Varies As T Bartleby




Prove That 8 1 Sin Pi 8 1 Sin 3pi 8 1 Sin 5pi 8 1 Sin 7pi 8 1 S E E Solution
If sin^2θcos^42θ=3/4, qe (0,π/2) then sum of all values of θ is(a) π/2(b) π(c) 3π/2(d) None of theseDownloads our APP for FREE Study Material ,Video ClaBut range of principal value of sin−1 is 2−π , 2π ie, −90o,90o Hence y = 1o is not possible Now, siny = sin1o siny = sin(180o −60o) siny = sin60o ∵ sin(180−θ)= sinθ siny = sinK π π / 2 Inflection point k π is to precalculate a table of sine values, for example one value per degree, then for values inbetween pick the closest precalculated value, or linearly interpolate between the 2 closest values to approximate it This allows results to be looked up from a table rather than being calculated in real time




Pi Wiskunde Wikipedia




Rd Sharma Solutions For Class 11 Chapter 7 Values Of Trigonometric Functions At Sum Or Difference Of Angles
The answer is $(1)^n$ And why is this wrong?2 dx from 0 to π/2 Integration is the inverse of differentiationGiven a derivative of a function, the process of finding the original function is called integration Answer The value of the integral (1 2cos x) / (2 cos x)^{2} dx from 0 to π/2 is 1 / 2 Let's look into the solution step by stepWe know that the range of the principal value branch of sin1 is π/2, π/2 So, – π/2 ≤ y ≤ π/2 Hence, option (B) is the correct answer Question 14 tan1 √3 – sec1 (2) is equal to (A) π (B) – π/3 π/3 (D) 2π/3 Answer Let tan −1 (√3) = y, then tan y
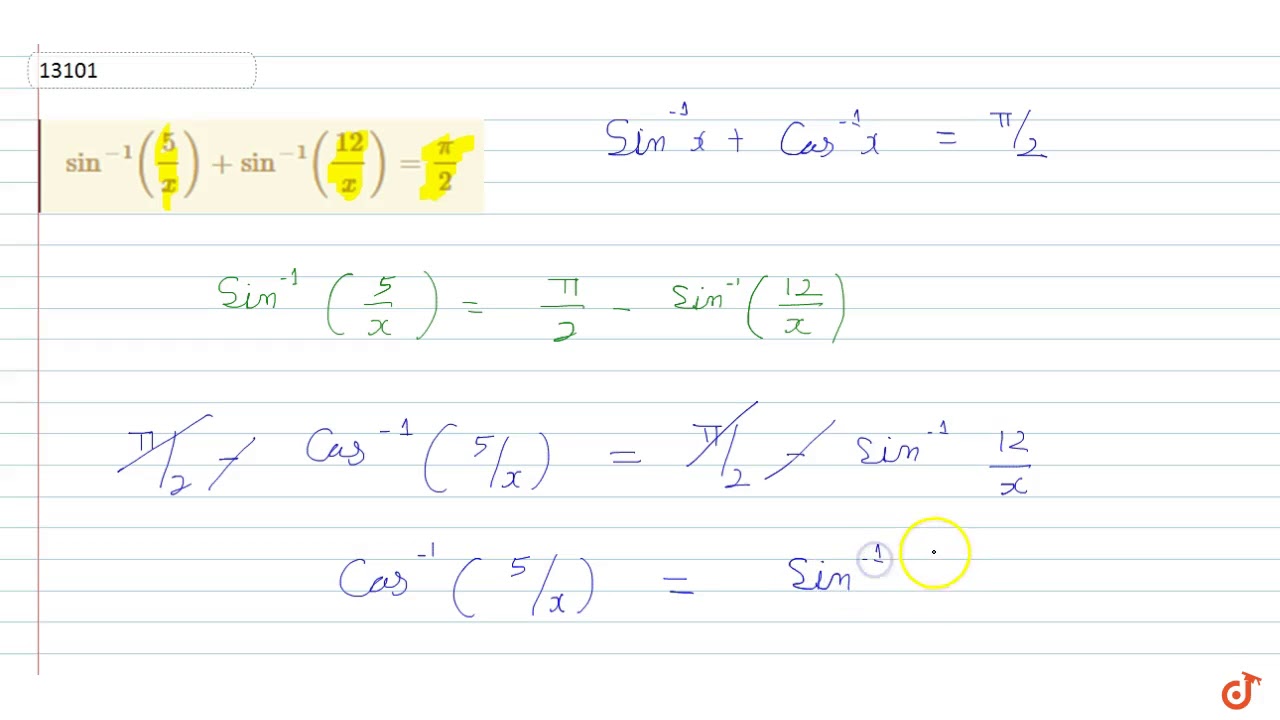



Sin 1 5 X Sin 1 12 X Pi 2 Youtube




5 Ways To Calculate Pi Wikihow
Soluciona tus problemas matemáticos con nuestro solucionador matemático gratuito, que incluye soluciones paso a paso Nuestro solucionador matemático admite matemáticas básicas, preálgebra, álgebra, trigonometría, cálculo y mucho másIf the minimum value of (sin − 1 x) 2 (cos − 1 x) 2 is k π 2 , then the value of k is A 4 B 6 C 8 D 1 0 Video Explanation Answer Correct option is C 8 f (x) = (sin Find the principal values of the following Question 1 sin1 (1/2) Solution Let sin1 (1/2) = y then, sin y = 1/2 Range of principal value for sin1 is π/2,π/2 and sin(π/6)=1/2 Therefore, principal value of sin1 (1/2)=π/6 Question 2 cos1 (√3/2) Solution




Prove That I Sin Pi 6 Cos Pi 6 Sqrt 3 4 Iii Cos 2 Pi 2 Sin 2 Pi 2 Sqrt 3 2




Packet 21 Trigonometric Identities Ppt Download
Welcome to sin π/2, our post aboutthe sine of π/2 radians For the sin of minus π/2 radians we use the abbreviation sin for the trigonometric function and write it as sin π/2 If you have been looking for what is sin π/2, or if you have been wondering about sin π/2 radians in degrees, then you are right here, too In this post you can find the sin π/2 value, along with identitiesNotation Several notations for the inverse trigonometric functions exist The most common convention is to name inverse trigonometric functions using an arc prefix arcsin(x), arccos(x), arctan(x), etc (This convention is used throughout this article) This notation arises from the following geometric relationships citation needed when measuring in radians, an angle of θSin (nπ/2) can not be given a general value When n is even, nπ/2 becomes an integral multiple of π Thus, sin (nπ/2) will be zero If n is of the form 4k1,
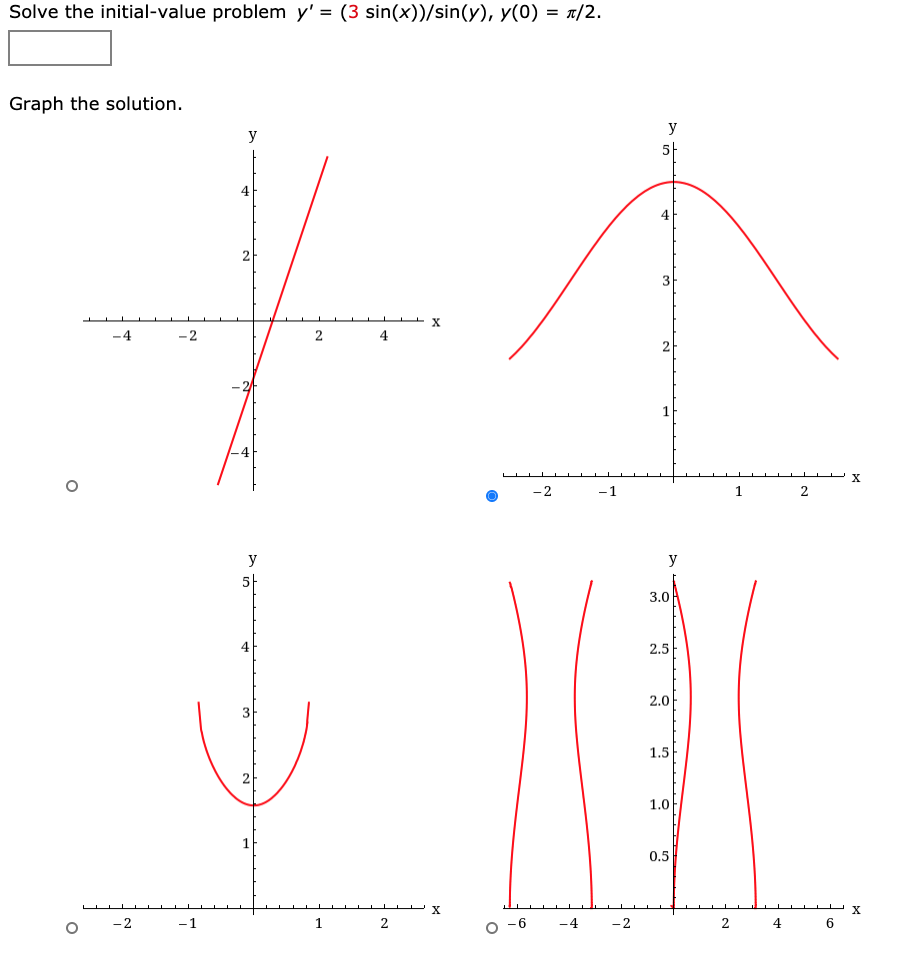



Solve The Initial Value Problem Y 3 Chegg Com




Unit Circle Sine And Cosine Functions Precalculus Ii
Ex 22, Find the values of sin (π/3 −"sin−1" (−1/2)) is equal to (A) 1/2 (B) 1/3 1/4 (D) 1 Solving sin1 ((−𝟏)/𝟐) Let y = sin1 ((−1)/2) y = − sin1 (1/2) y = − 𝛑/𝟔 We know that sin−1 (−x) = − sin −1 x Since sin 𝜋/6 = 1/2 𝜋/6 = sin−1 (𝟏/𝟐) Thus, sin−




Find Each Value Tofour Decimal Places 1 Sin 30 Gauthmath




Evaluate Sin Pi 2 Sin 1 Sqrt 3 2




Sin Pi 2 X Sin Pi X 2 Cos 3pi 2 X Cos 2pi X 2




Trigonometric Functions Angles Tables Degree Radians Sin Cos Tan




Find Exact Value Of Cos 2 Pi 8 Youtube




Trigonometry Ppt Download




Cos Pi 2




Inverse Trigonometric Functions Ppt Download




The Value Of Sin 1 Sin Pi 3 X X 2 K 2 Kx Cos 1 Cospi 6 X X 2 K 2 Kx Where K2 0 Is




Prove That Tan Pi2 X Sec Pi X Sin X Sin Pi X Cot 2pi X Pi2 X 1




The Value Of Cos P 2 2 Cosp 2 3 Cosp 2 10 Sinp 2 10 Brainiak




If Sin 1 X Sin 1 Y 2pi 3 Then Value Of Cos 1 X Cos 1 Y Is
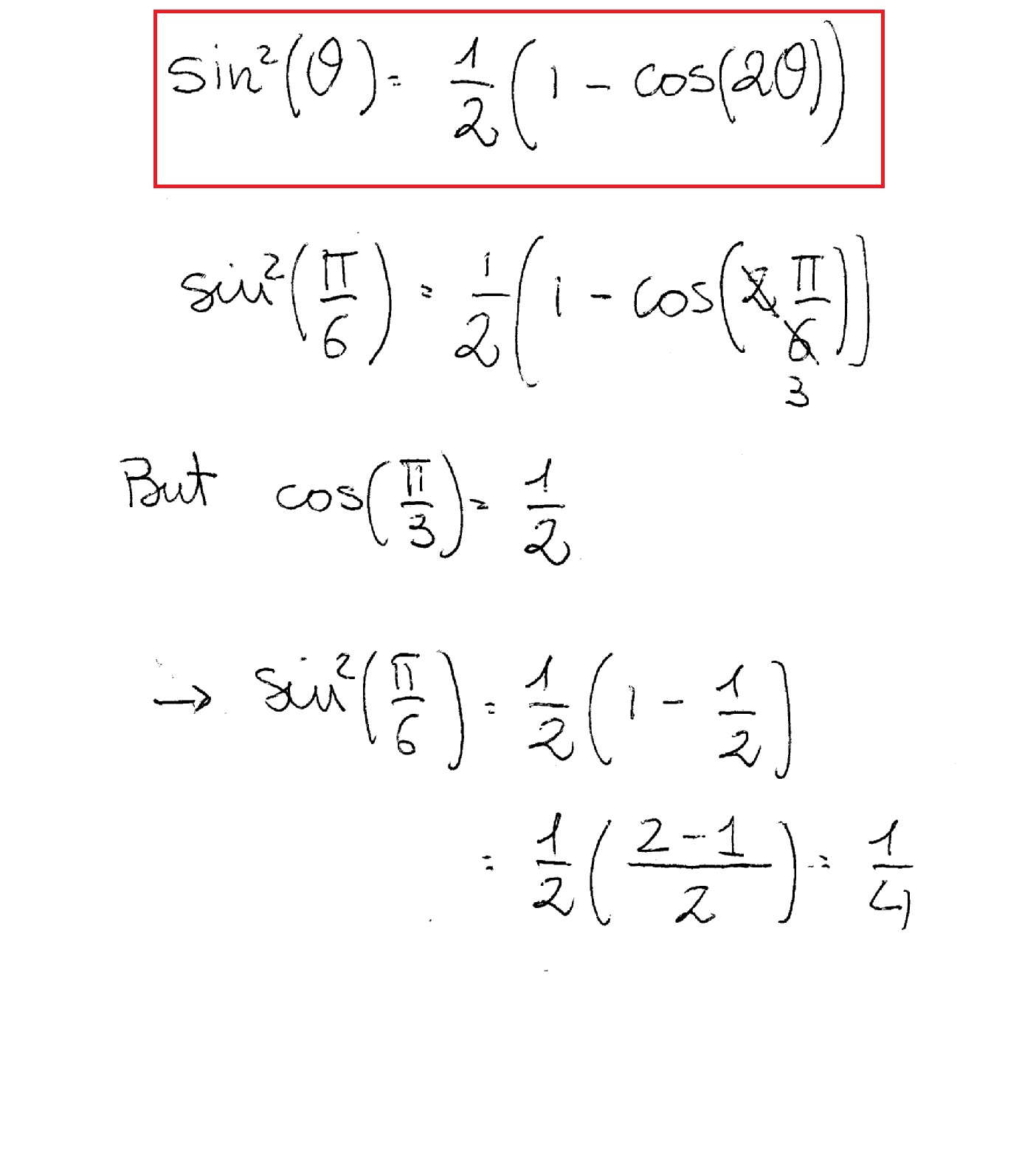



How Do You Use The Half Angle Formula To Simplify Sin 2 Pi 6 Socratic




Ex 3 3 6 Prove That Cos Pi 4 X Cos Pi 4 Y Chapter 3




The Inverse Function Of Y Sinx On 0 2p The Inverse Function Of Y Sinx On P 2 P Is X P Arcsiny Use This Article To Clarify The Relationship Between The Inverse Trigonometric Function Programmer Sought




Cos Pi 2




Evaluate The Following Sin Pi 2 Sin 1 1 2 Youtube




Sin 2 Pi 6 Cos 2 Pi 3 Tan 2 Pi 4 1 2 Youtube



1
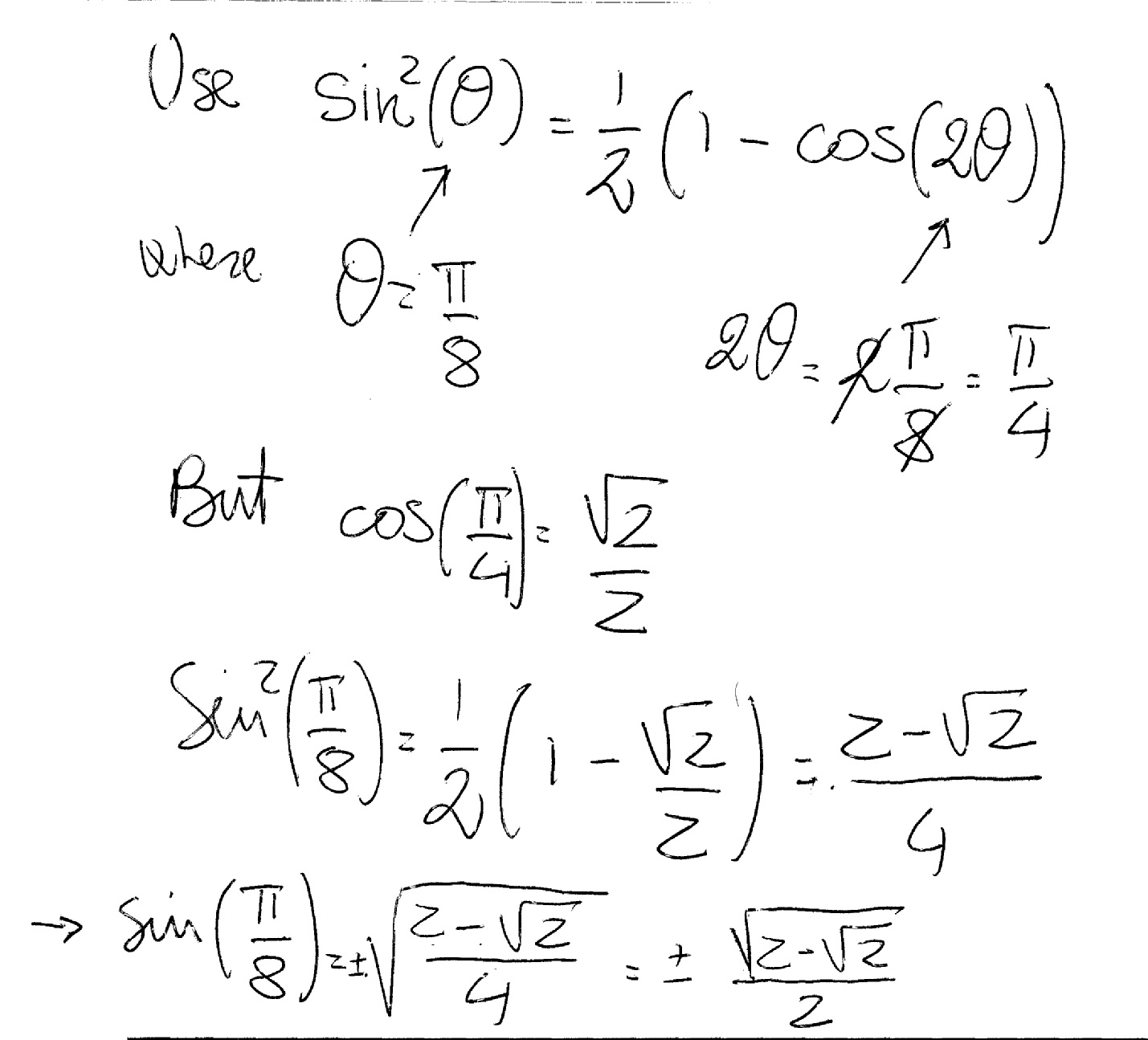



How Do You Use The Half Angle Formula To Simplify Sin 2 Pi 8 Socratic



How To Solve Sin P 14 Sin 3p 14 Sin 5p 14 Quora




Maximum Value Of Sinxsin Pi 3 X Sin Pi 3 X Maths Trigonometric Functions Meritnation Com




Iit 1994 Show That If Sin Pi 2n Cos Pi 2n Sqrt N 2 Then N Lies Between 4 And 8 Youtube




Solving Sinusoidal Equations Of The Form Sin X D Video Khan Academy




Cofunction Identities In Trigonometry With Proof And Examples Owlcation




The Value Of Cos P 2 I Sin P 216 Gauthmath




Solve 11sin Theta 2 2 For A Value Of Theta When 0 Theta Pi 2 Socratic




Ch Ppt Download




Let N Be A Positive Integer Such That Sin Pi 2 N Cos Pi 2 N Sqrt N 2 Then Youtube




Find The Value Of Sinpi 14sin3pi 14sin5pi 14
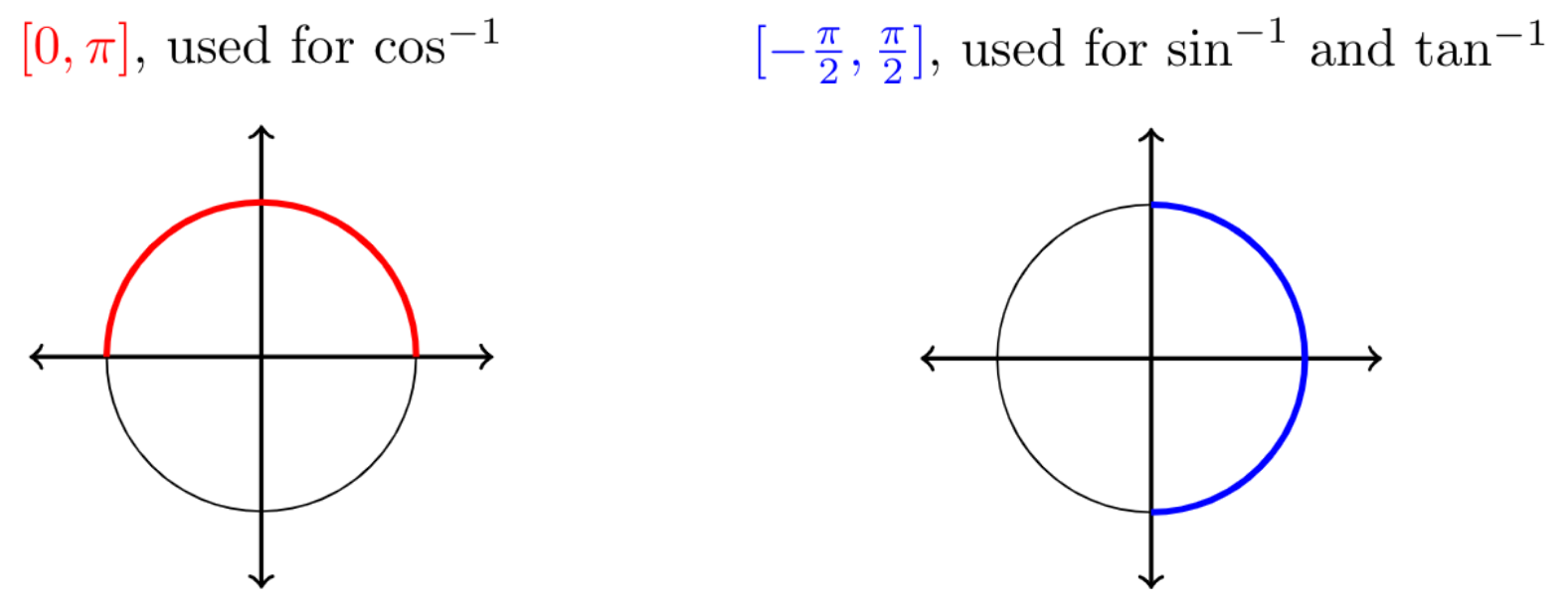



Mfg Inverse Trigonometric Functions




If Sin X 5 3 And Pi2 X Pi Find The Value Of Sin X2




Solution Evaluate The Integral Of Sin 6 Xdx From 0 To P 2



Law Of Sine Laws And Formulas Properties Of Trigonometric Functions 29 7 Sideway Output To




Sine Wikipedia




Rd Sharma Solutions For Class 11 Chapter 7 Values Of Trigonometric Functions At Sum Or Difference Of Angles




The Value Of T A Nthetasin Pi 2 Theta Cos Pi 2 Theta Is 1 B 1 C 1 2sin2theta D None Of These
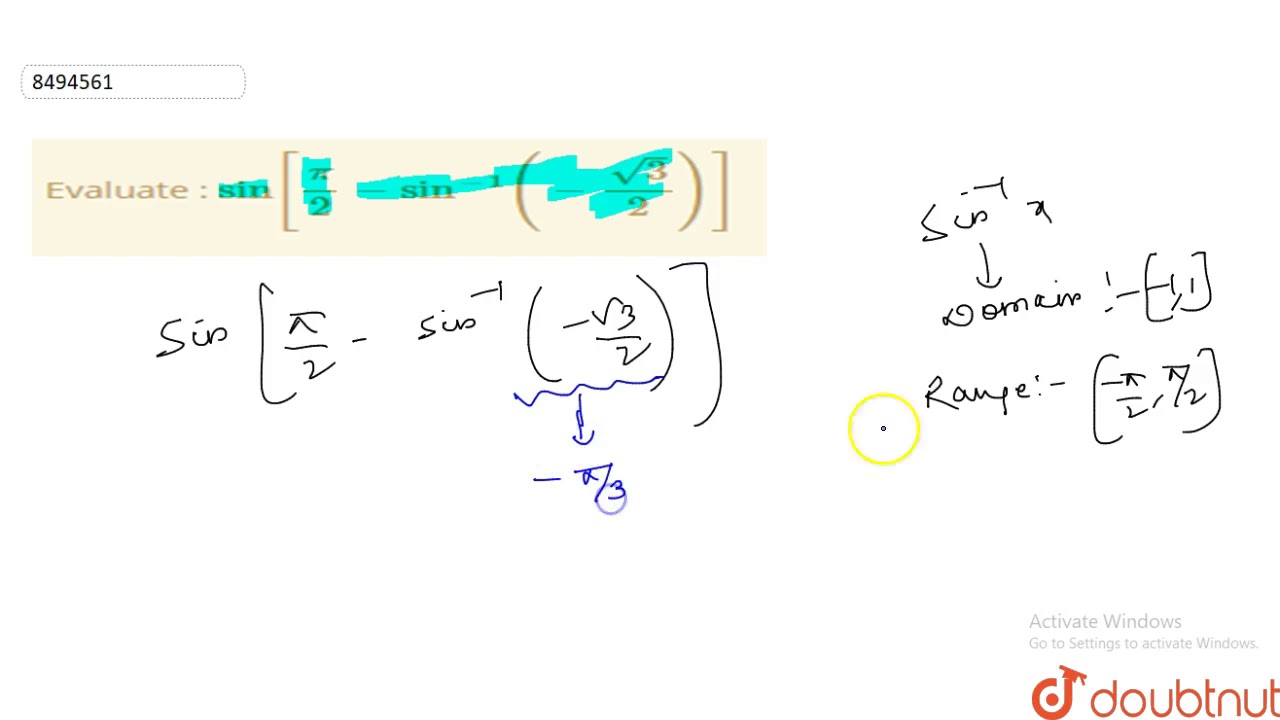



Evaluate Sin Pi 2 Sin 1 Sqrt 3 2 Youtube



How Do You Prove Cos X Pi 2 Sin X Socratic




Given Sin A 8 17 And Cos A 0 Evaluate Si Nfra Gauthmath




Find The Exact Value Of Arctan Sin Pi Divided By Two For Full Credit Explain Your Reasoning Brainly Com




Sin P 2 X Sin P X Cos 3p 2 X Cos 2p X Brainly In




Proved That 2 Sin P 4 Theta Costheta Sintheta Brainly In




Value For Sin Pi By 2 Brainly In
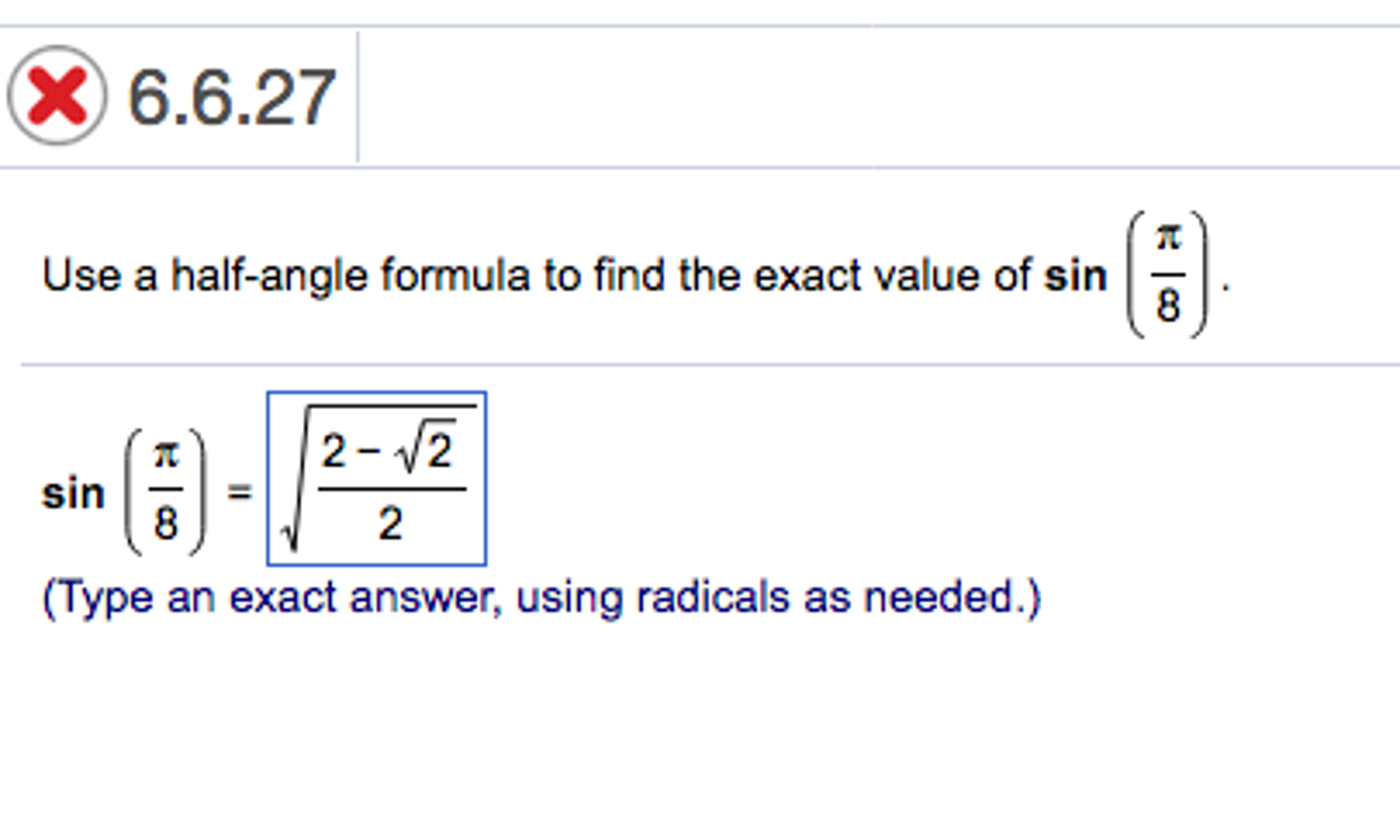



Use A Half Angle Formula To Find The Exact Value Of Chegg Com




Ex 3 3 1 Prove Sin2 Pi 6 Cos2 Pi 3 Tan2 Pi 4 1 2




The Value Of Sin Pi7 Sin 2pi 7 Sin 3pi 7 Is Equal To
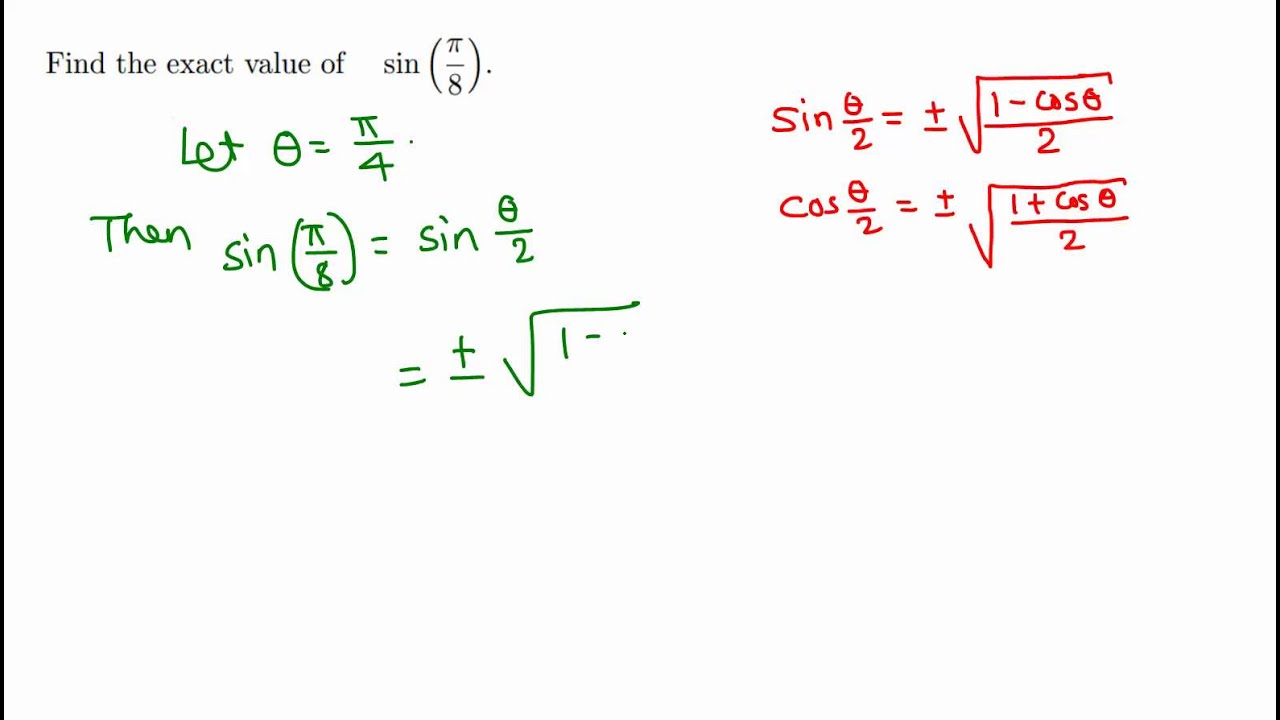



Trigonometry Exact Value Of Sin Pi 8 Sin 22 5 Youtube
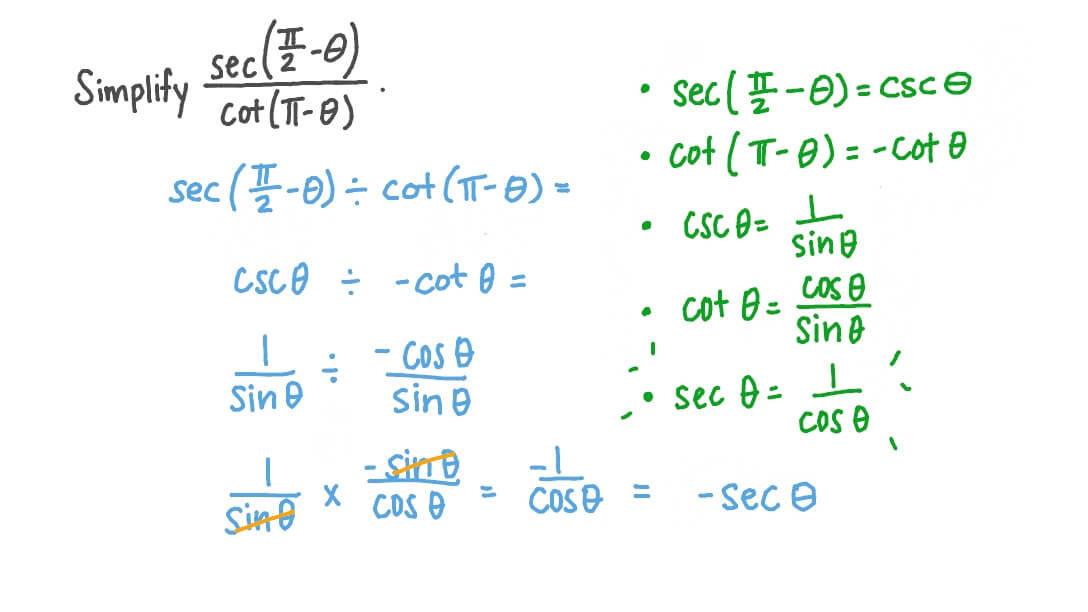



Question Video Using Periodic And Cofunction Identities To Simplify A Trigonometric Expression Nagwa




Sin P 8 Sin 7p 8 Cos 3p 8 Cos 5p 8 2 Sin 2 P 8
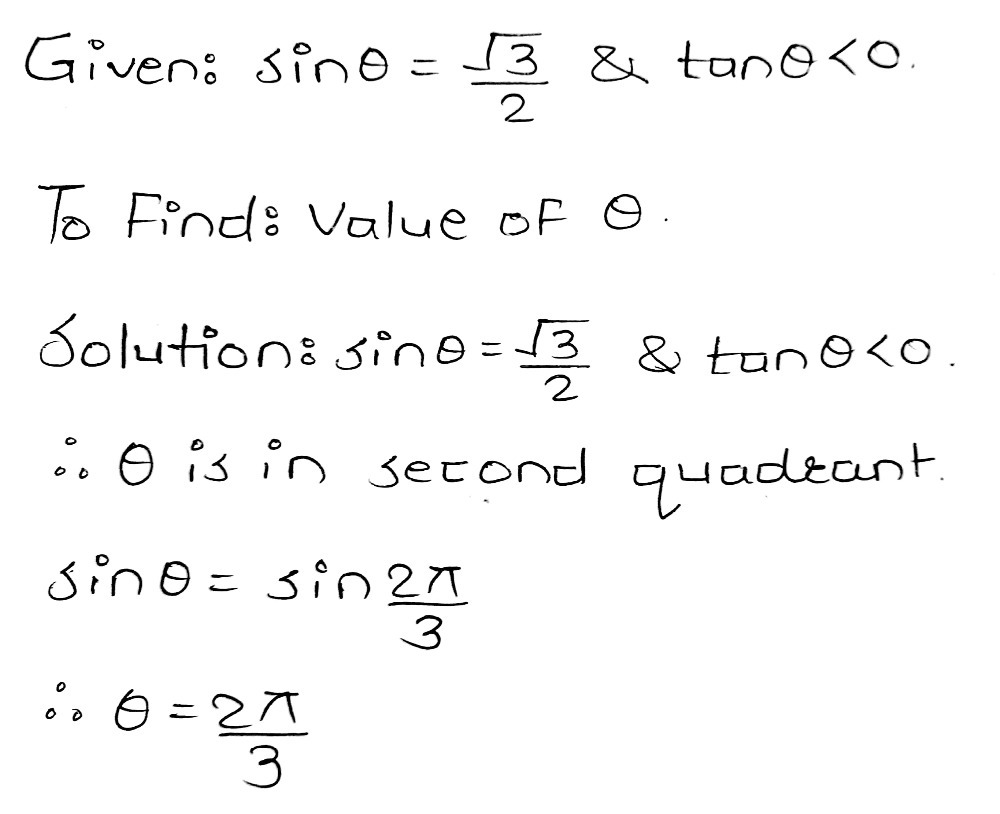



Sin 8 Frac Square Root Of 32 And Tan 8 Lt 0 A Gauthmath
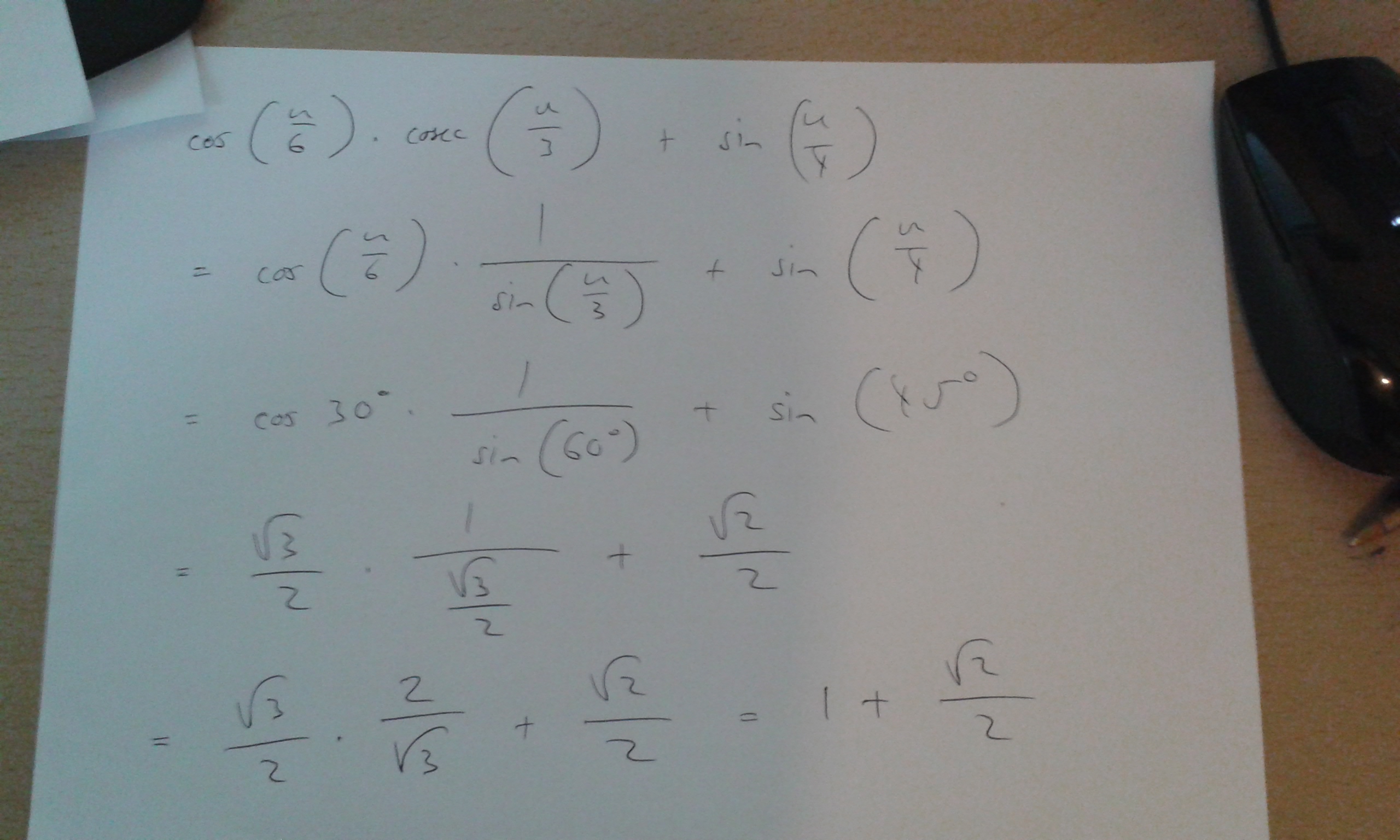



How Do You Determine The Exact Value For Cos Pi 6 Csc Pi 3 Sin Pi 4 Socratic



Solved Consider The Value Of The Trigonometric Function Sin 6 It S Value Is Greater Than 1 Because The Hypotenuse Of A Right Triangle Is The Sho Course Hero




The Range Of F X Sin Pi 2 X Is Here X Denotes Greatest Integer Lt X




Pin On Math




Evaluate The Following I Sin Pi 2 Sin 1 1 2 Ii Sin Pi 2 Sin 1 Sqrt3 2




Then X B And X A Are Substituted A Result Is Subtracted From Scholr




Ex 2 2 Find Sin Pi 3 Sin 1 1 2 Class 12 Ncert




Sin Pi 2 X Cot Pi 2 X Sinx Trigonometric Identities With Related Acute Angle Youtube




Solve Limit X Sin P X When X Tends To Infinity




How To Find The Value Of Sin 8 Maths Trigonometric Functions Meritnation Com



1



1




List Of Trigonometric Identities Wikipedia




What Is The Meaning Of This Expression Mathematics Stack Exchange
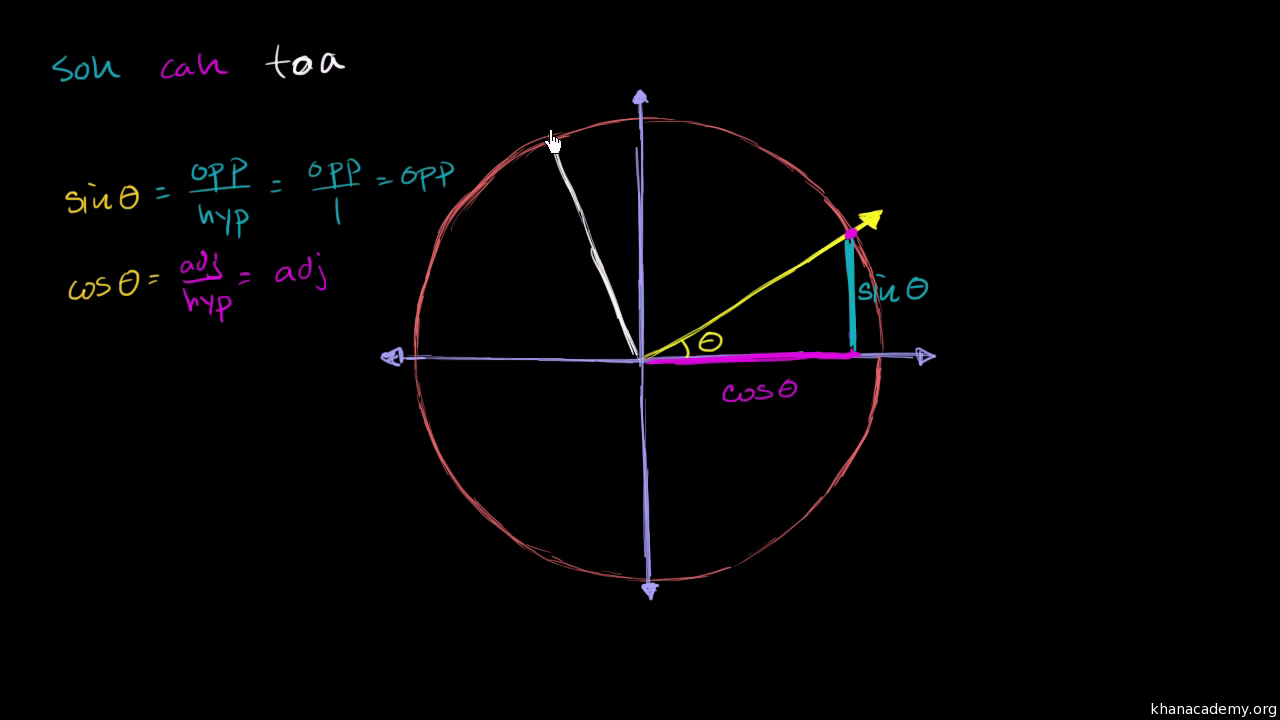



Sine Cosine Identities Periodicity Video Khan Academy




If Sina 3 5 And Pi 2 A Pi Find Cos A Maths Trigonometric Functions Meritnation Com
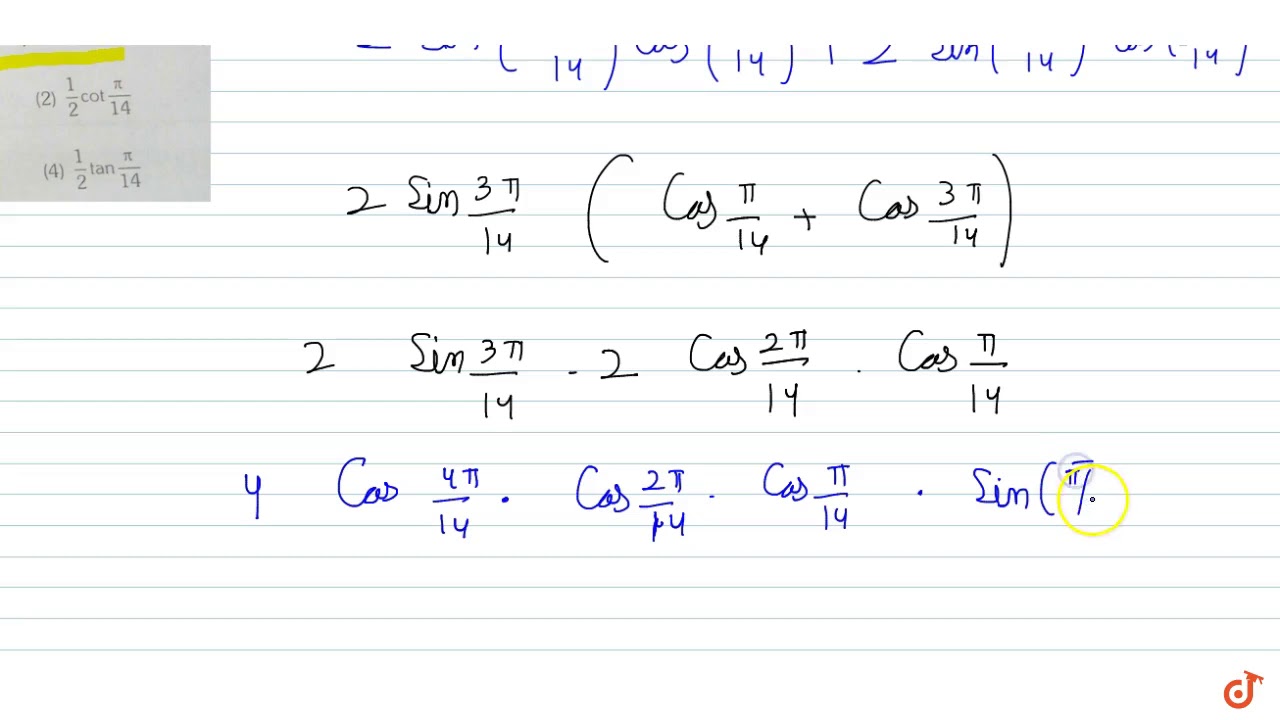



The Value Of Sin Pi 7 Sin 2pi 7 Sin 3pi 7 Is Youtube
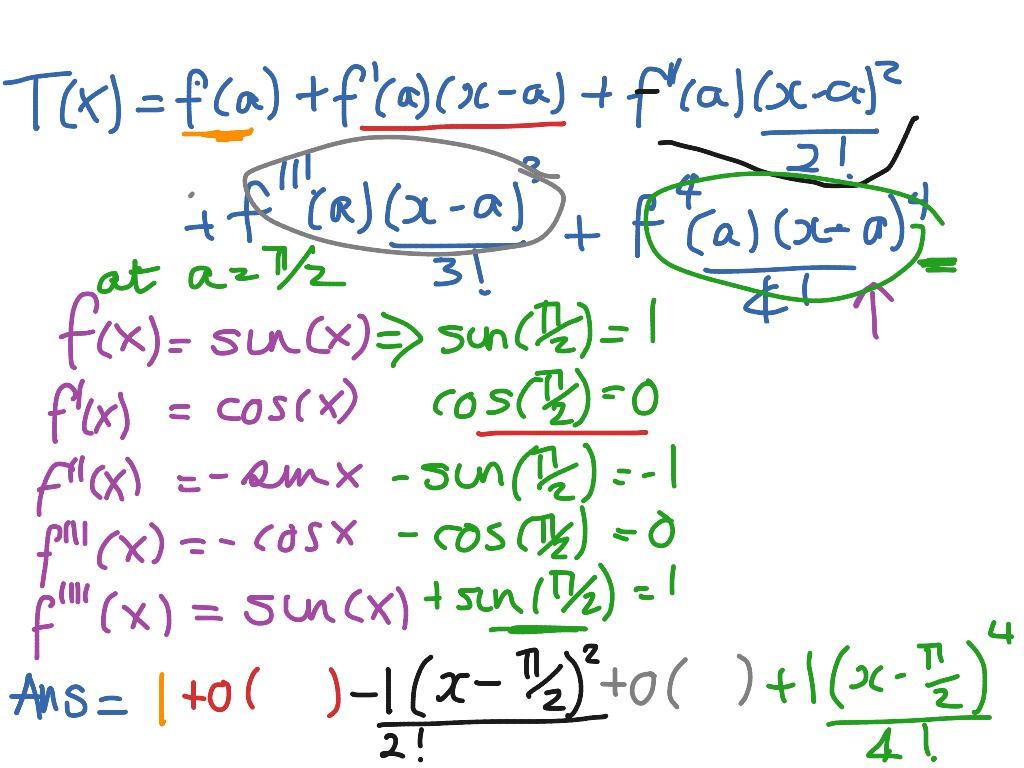



Taylor Series Of Sin X At Pi 2 Math Calculus Taylor Series Showme




How To Find The General Solution Of Sin Left Theta Frac Pi 6 Right Cos 3 Theta Mathematics Stack Exchange




Ex 2 2 16 Find Sin 1 Sin 2pi 3 Chapter 2 Ncert Ex 2 2




If X R Cos Pi 2 R I Sin Pi 2 R Z T Cos Pi 3 T I Sin Pi 3 T Where R 1 2 Youtube




How N Pi 1 N Pi 6 N Pi Pi 6 And N Pi 1 N Pi 6 N Pi Pi 6 Mathematics Stack Exchange




Value Of Tan Pi 2 Mathematics Stack Exchange



1




Finding Trig Values Using Angle Addition Identities Video Khan Academy




Solve Sin 1 1 X 2 Sin 1 X Pi 2 Then X Is Trigonometry
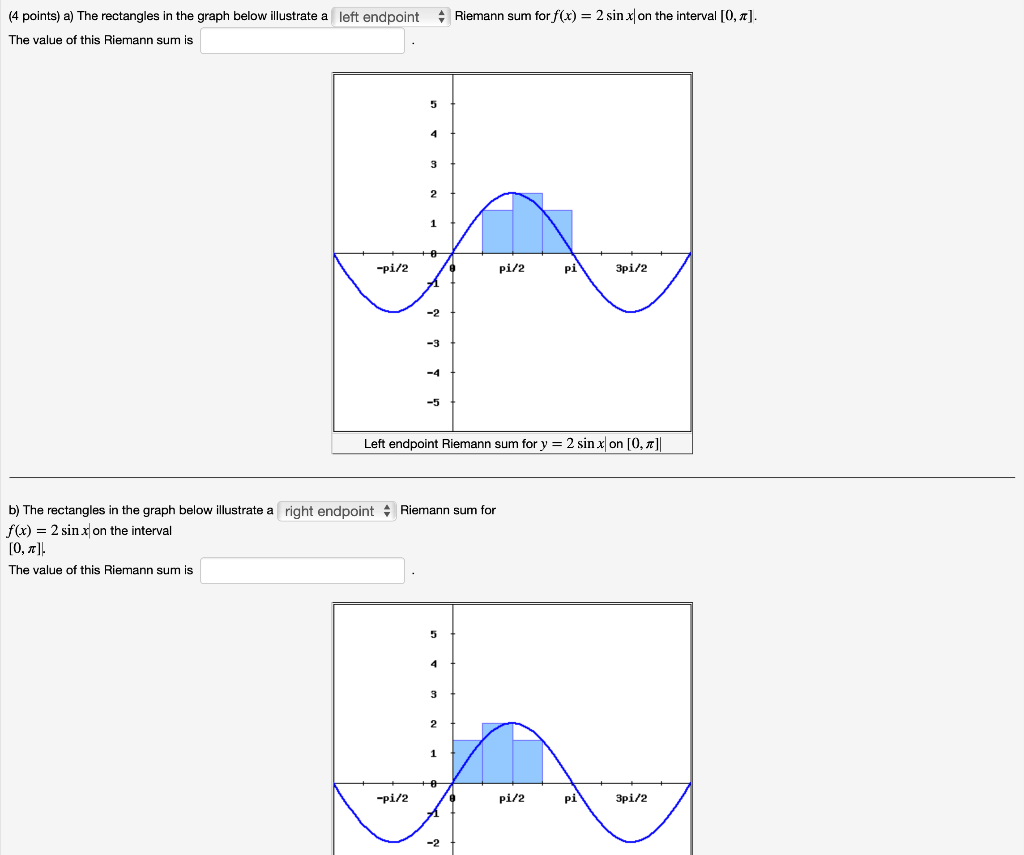



Riemann Sum Forf X 2 Sin Xl On The Interval 0 Chegg Com




Ex 3 3 6 Prove That Cos Pi 4 X Cos Pi 4 Y Chapter 3




The Positive Integer Value Of N 3 Satisfing The Equation Frac 1 Sin Left Frac Pi N Right Frac 1 Sin Left Frac 2pi N Right Frac 1 Sin



0 件のコメント:
コメントを投稿