So, (1) Any line with positive slope through (2,1) meets the condition for example f (x) = 3(x − 2) 1 has f '(x) = 3 > 0 for all x ≠ 2 and also for x = 2 graph {y1=3 (x2) 1907, 919, 245, 31} Replace 3 with any positive number for another exampleF x = x ^ { 2 } 6 x 8 f x = x 2 − 6 x 8 The equation is in standard form The equation is in standard form xf=x^ {2}6x8 x f = x 2 − 6 x 8 Divide both sides by x Divide both sides by x \frac {xf} {x}=\frac {\left (x4\right)\left (x2\right)} {x} HSBC244 has shown a nice graph that has derivative #f'(3)=0# Here are couple of graphs of functions that satisfy the requirements, but are not differentiable at #3# #f(x) = abs(x3)5# is shown below graph{y = abs(x3)5 14, 25, 616, 1185} #f(x) = (x3)^(2/3) 5# is shown on the next graph
Solution Graph The Piecewise Function Show All Work F X X If X Amp 04 0 And 0 If 0 Lt X Lt 5 And 2x 10 If X Amp 05 5 State Whether The Function Is Continuous If It Is
What does f'(x) 0 mean
What does f'(x) 0 mean- For x < 0 , f(x) = 1 – x We find the points to be plotted when x < 0 For x = 0 , f(x) = 1 Hence, point to be plotted is (0,1) For x > 0 , f(x) = x 1 We fi (टीचू) Maths† x = a is a minimum if f0(a) = 0 and f00(a) > 0;
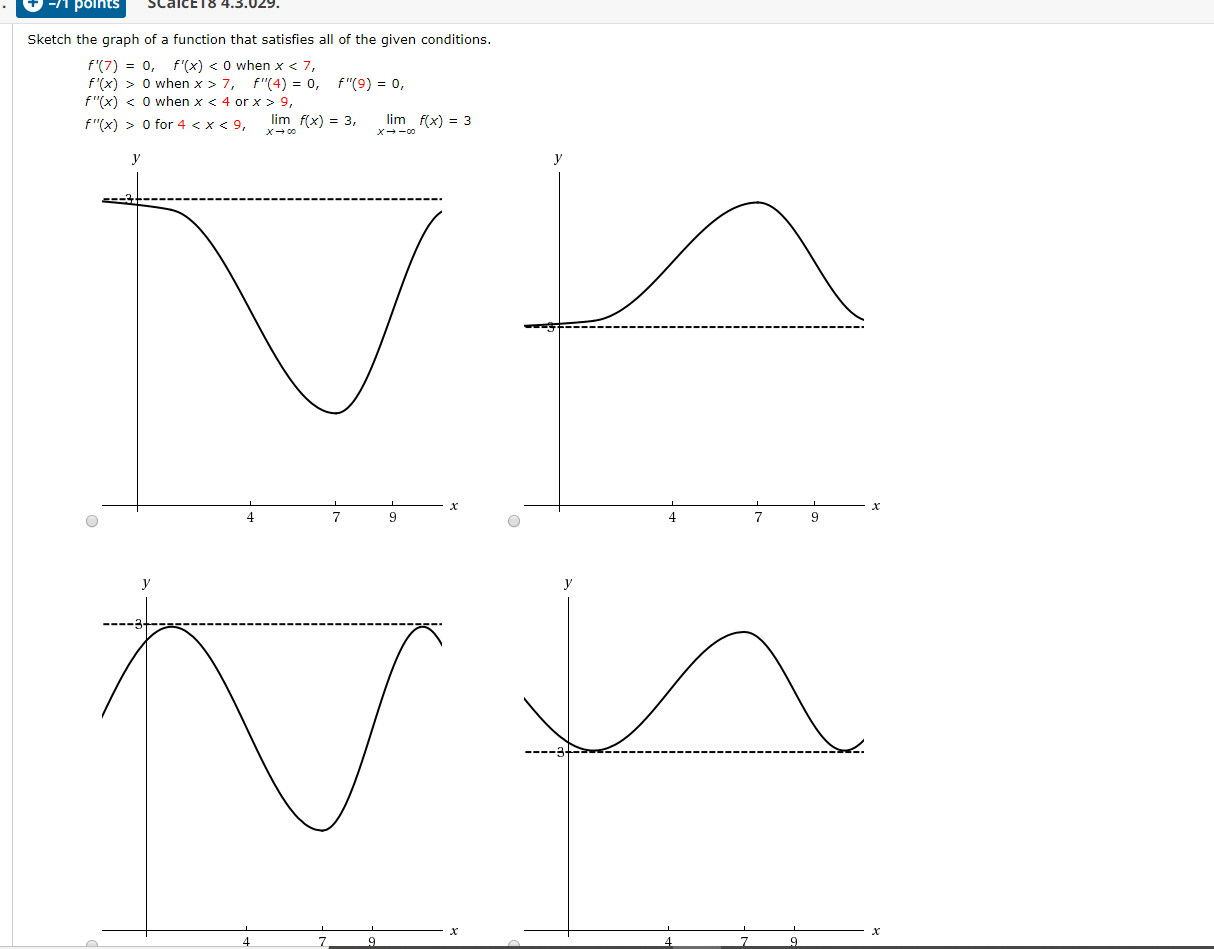



1 Polnts Scalce18 4 3 029 Sketch The Graph Of A Chegg Com
How to tell where f(x) greater than 0 or f(x) less than 0 How to tell where f(x) greater than 0 or f(x) less than 0(a)Find the derivative f0(x) lim h!0 f(x h) f(x) h = lim h!0 4 xh 4 x h = lim h!0 4x 4(xh) x(xh) h = lim h!0 4h hx(x h) = lim h!0 4 x(x h) = 4 x2 (b)Find and interpret f0(5) f0(5) = 4 52 = 4 25 The slope of f at x = 5 is 4 25 (c)When x = 5, is the graph of f(x) increasing, decreasing, or neither?F(x) = (c) Use calculus to find the exact maximum value of f(x) f(x) = (d) Use a graph of f '' to estimate the xcoordinates of the inflection points (Round your
0 (b) Explain the shape of the graph by computing the limit as x ?GRAPH OF f(x) = x^3 f(x) = x^3 graph how to draw graph of f(x)=x^3 y = x^3 graphNCERT CLASS 11 MATHS SOLUTIONS ex 23SUBSCRIBE TO MY CHANNEL TO GET MORE UPDACos x about x =0 Use this series and the series for sin ,()x2 found in part (a), to write the first four nonzero terms of the Taylor series for f about 0x = (c) Find the value of f ()6 ()0 (d) Let Px4( ) be the fourthdegree Taylor polynomial for f about 0x = Using information from the graph of yf x= ()5 shown above, show that ( ) ( ) 4 11
Steps for Solving Linear Equation f ( x ) = 1 \frac { 2 } { x 1 } , s f ( x) = 1 − x 1 2 , s Multiply both sides of the equation by x1 Multiply both sides of the equation by x 1 fx\left (x1\right)=x12 f x ( x 1) = x 1 − 2 Use the distributive property to multiply fx by x1 Transcript Ex 51, 8 Find all points of discontinuity of f, where f is defined by 𝑓(𝑥)={ (𝑥/𝑥, 𝑖𝑓 𝑥≠0@&0 , 𝑖𝑓 𝑥=0)┤ Since we need to find continuity at of the function We check continuity for different values of x When x = 0 When x > 0 When x < 0 Case 1 When x = 0 f(x) is continuous at 𝑥 =0 if LHL = RHL = 𝑓(0) Since there are two differentThe expression f(0) represents the yintercept on the graph of f(x) The yintercept of a graph is the point where the graph crosses the yaxis This



Yahoo Answers 04 09 Geogebra




How Many Values Of C Is The Derivative Of The Function Equal To Its Average Rate Of Change Mathematics Stack Exchange
Let us start with a function, in this case it is f(x) = x 2, but it could be anything f(x) = x 2 Here are some simple things we can do to move or scale it on the graph We can move it up or down by adding a constant to the yvalue g(x) = x 2 C Note to move the line down, we use a negative value for C C > 0 moves it up;F 0(x) = k f (x) Solution Multiply the equation above f 0(x) − kf (x) = 0 by e−kx, that is, f 0(x) e−kx − f (x) ke−kx = 0 The lefthand side is a total derivative, f (x) e−kx 0 = 0 The solution of the equation above is f (x)e−kx = c, with c ∈ R Therefore, f (x) = c ekx C7 Consider the following 1 x 1 lim x x 1 Use the graph to find the limit (if it exists)
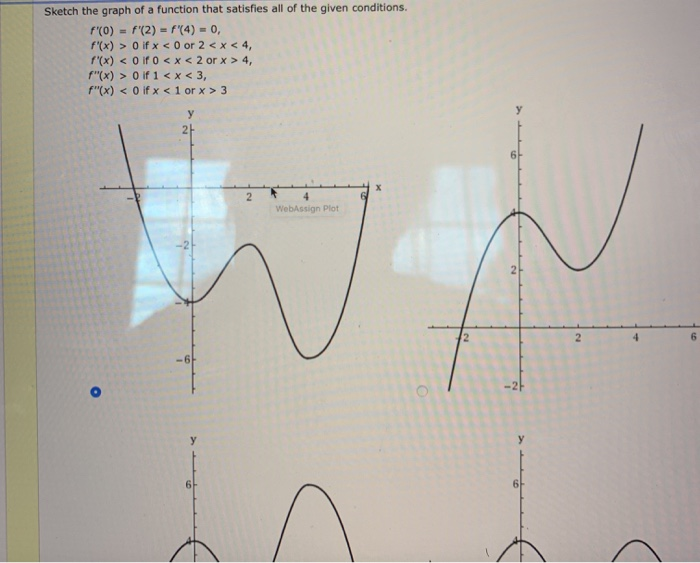



Sketch The Graph Of A Function That Satisfies All Of Chegg Com
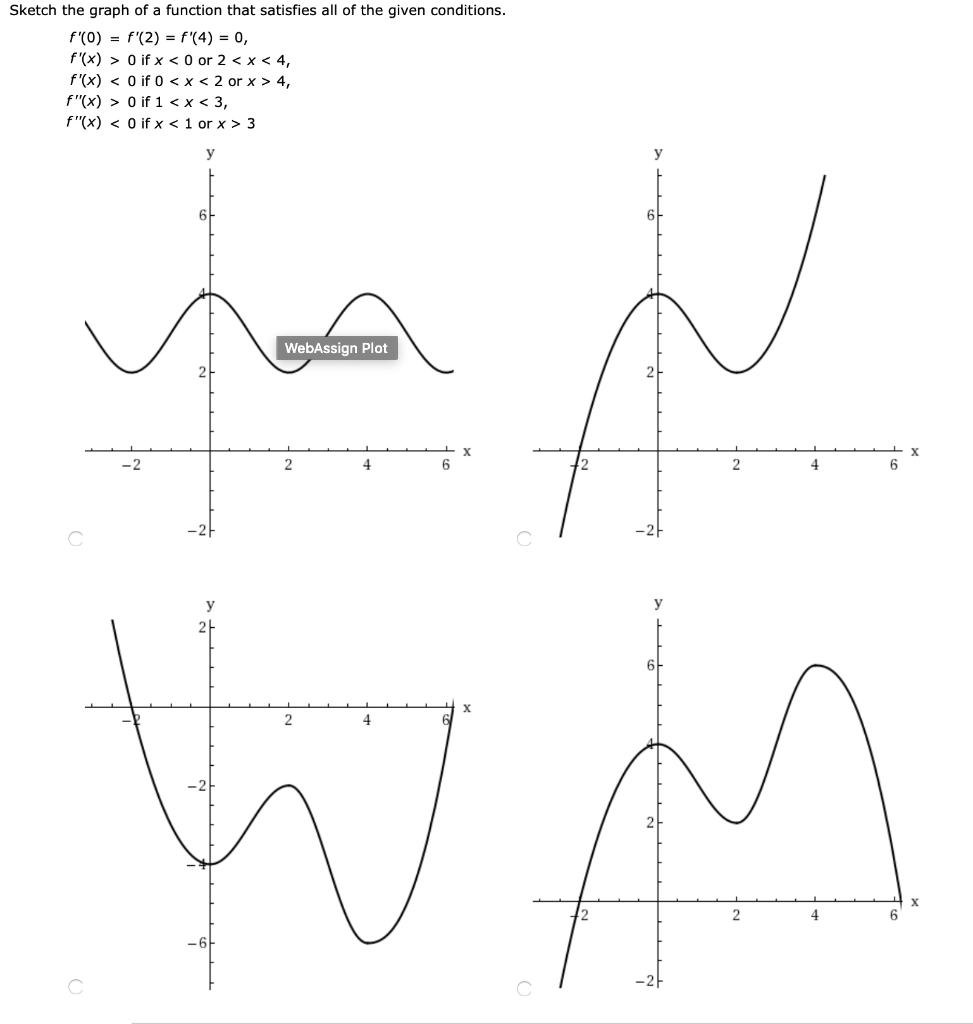



Sketch The Graph Of A Function That Satisfies All Of Chegg Com
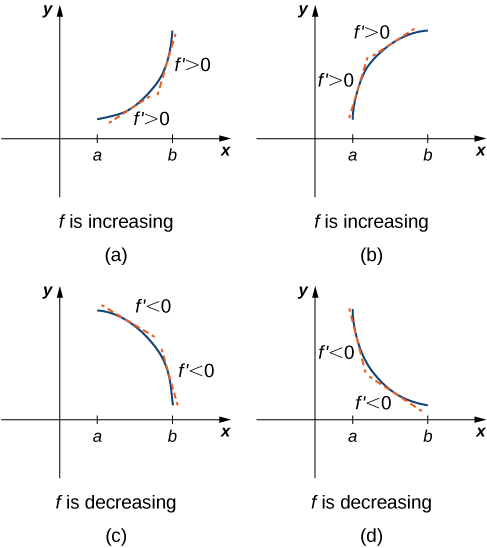
Δx 0 answer We've computed −that f (x) = 1 Is this correct?If f′(x) > 0 for all x ∈(a,b), then f is increasing on (a,b) If f′(x) < 0 for all x ∈(a,b), then f is decreasing on (a,b) First derivative test Suppose c is a critical number of a continuous function f, then Defn f is concave down if the graph of f lies below the tangent lines to f Defn f is concave up if the graph of fF0(x) = (2x if x>0;




Section 3 4 Concavity And The Second Derivative Test Ppt Download



Www Hershey K12 Pa Us Cms Lib Pa Centricity Domain 528 Test review mc not graded key Pdf
0 if x 0 For x>0, the derivative is f0(x) = 2xas above, and for xFor example, if f is a function that has the real numbers as domain and codomain, then a function mapping the value x to the value g(x) = 1 / f(x) is a function g from the reals to the reals, whose domain is the set of the reals x, such that f(x) ≠ 0 The range of a function is the set of the images of all elements in the domainHow might we check our x2 0 work?




How To Use Graph To Determine Where F X 0 And F X 0 Mathematics Stack Exchange
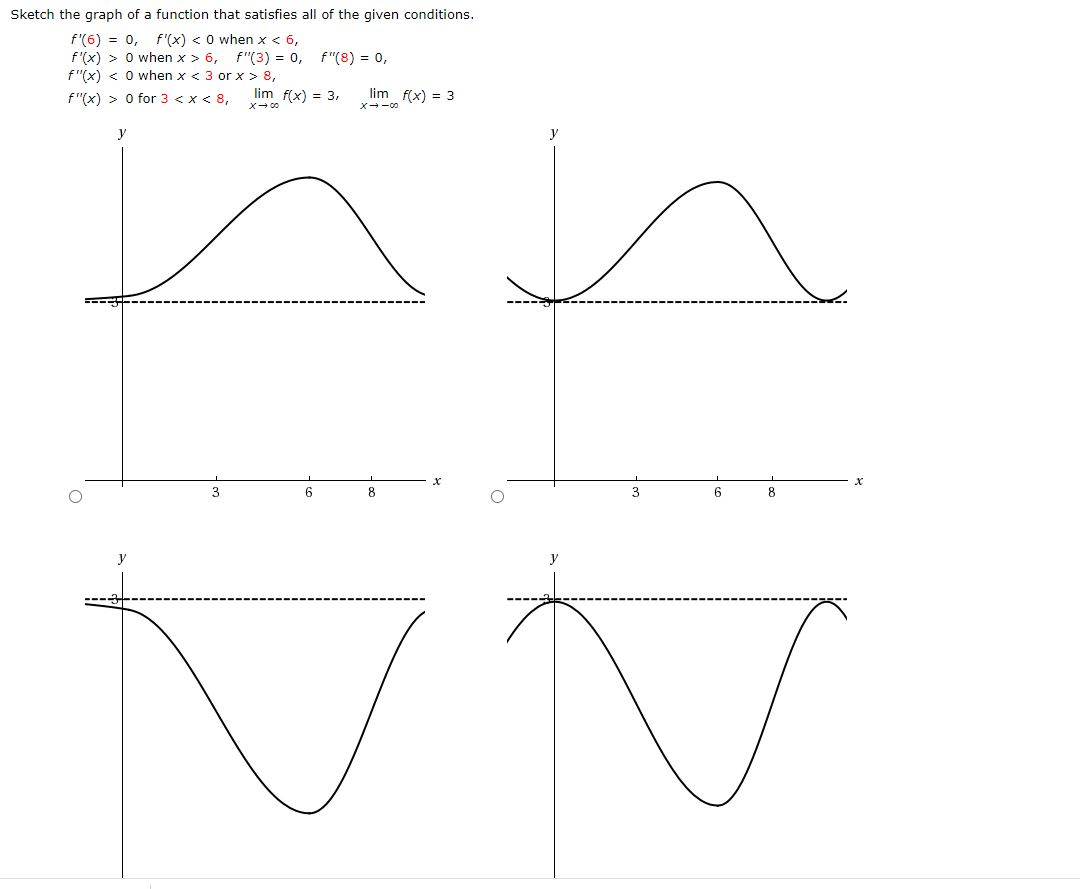



Sketch The Graph Of A Function That Satisfies All Of Chegg Com
A function may be thought of as a rule which takes each member x of a set and assigns, or maps it to the same value y known at its image x → Function → y A letter such as f, g or h is often used to stand for a functionThe Function which squares a number and adds on a 3, can be written as f(x) = x 2 5The same notion may also be used to show how a function affects particular valuesAnswer to Graph f(x) = 3^x 1 By signing up, you'll get thousands of stepbystep solutions to your homework questions You can also ask yourThis is an absolute value function It forms a v shaped graph For positive xvalues, and zero, it is a line with a yintercept of zero and a slope of one y = x if x > 0 or x = 0 For negative xvalues it is a line with a yintercept of zero and a slope of negative one y = x if x < 0



Web Ma Utexas Edu Users Jdanciger Fall11 Hw2 Soln Pdf
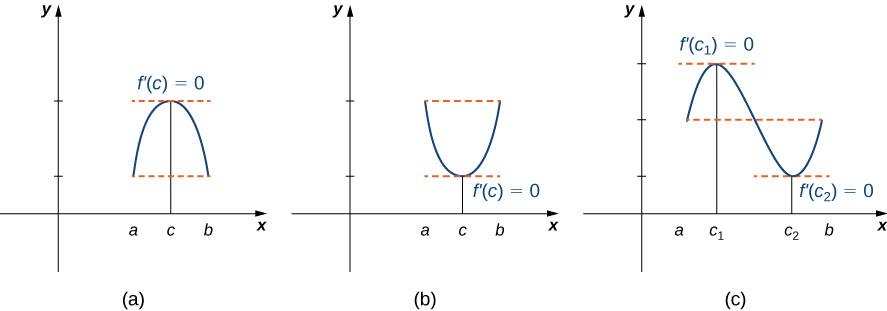



4 2 The Mean Value Theorem Mathematics Libretexts
Let f be continuous on an open interval (a,b) that contains a critical xvalue 1) If f'(x) > 0 for all x on (a,c) and f'(x)0 for all x on (c,b), then f(c) is a local maximum value 3) If f'(x) has the same sign on both sides of c, then f(cSince we're looking for f(x)=0, we're looking for y=0 since y and f(x) can be interchanged In other words, we are looking for the xintercept, since y=0 for all xintercepts So we substitute 0 in for f(x) and we get Now we solve for x Add 12 to both sides Divide both sides by 3 This will isolate xConsider the function below f(x) = x1/x, x >
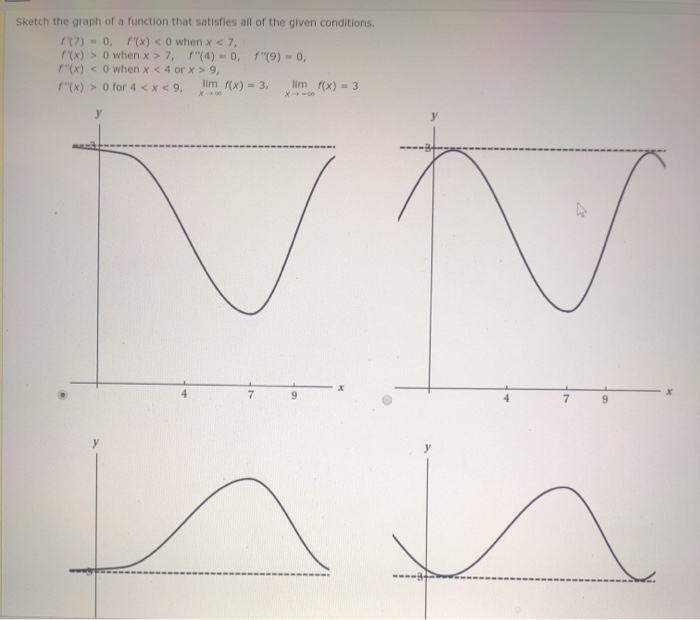



Sketch The Graph Of A Function That Satisfies All Of Chegg Com



Http Media Collegeboard Com Digitalservices Pdf Ap Apcentral Ap15 Calculus Ab Q5 Pdf
C < 0 moves it downFor the first case, we see that f(x) = 0 will solve our original function, since R x 0 0dx = 0 for all x In the second case, f0(x) = 1 2, so f(x) = 1 2 x C To get the value of C, notice in the original equation that if x = 0, then Z 0 0 f(x)dx = (f(0))2 ⇒ f(0) = 0 Thus, C = 0 So, we have two possibilities f(x) = 0 or f(x) = 1 2 x 30 For f ( x) ∗ f ′ ( x) < 0 either f ( x) is positive and f ′ ( x) is negative or vice versa I can see if f ( x) > 0 by seeing if the graph at x is a above or below the xaxis I can see if f ′ ( x) > 0 by seeing if at x the graph is increasing or not So I look for the areas of the graph with it is either both above the xaxis and decreasing or below the xaxis and increasing
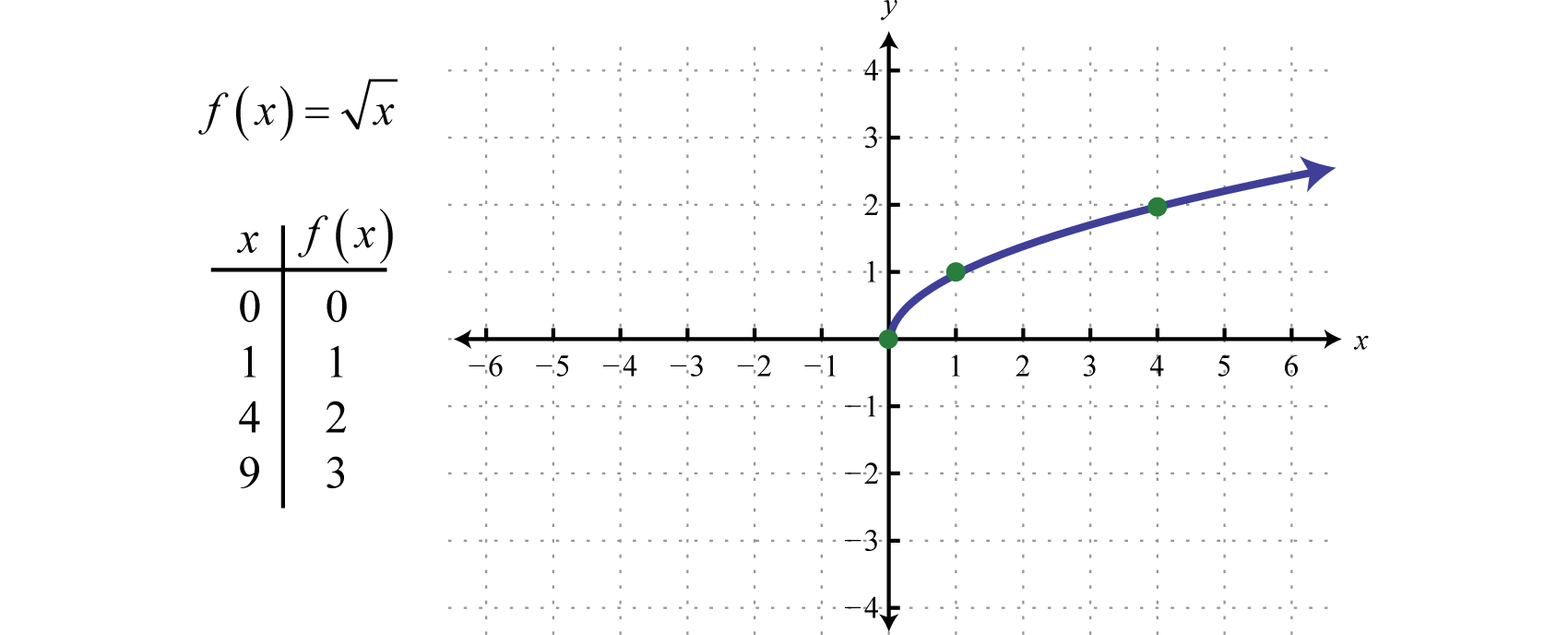



Graphing The Basic Functions




The Graph Of Y F X Is Shown Below What Are All Of The Real Solutions Of F X 0 Brainly Com
Graph f (x)=0 f (x) = 0 f ( x) = 0 Rewrite the function as an equation y = 0 y = 0 Use the slopeintercept form to find the slope and yintercept Tap for more steps The slopeintercept form is y = m x b y = m x b, where m m is the slope and b b is the yintercept y = m x b y = m x b Find the values of m m and b b using theSolution set of 'f(x)=0' xintercept(s) of graph Solution set of 'f(x)>0' xvalues corresponding to part of graph ABOVE xaxis Free, unlimited, online practiceFirst of all, f (x 0) is negative — as is the slope of the tangent line on the graph of y = 1 Secondly, as x 0 →∞ (ie as x 0 grows larger and larger), the x tangent line is less and less steep So x 1 should get closer to 0 as x 0
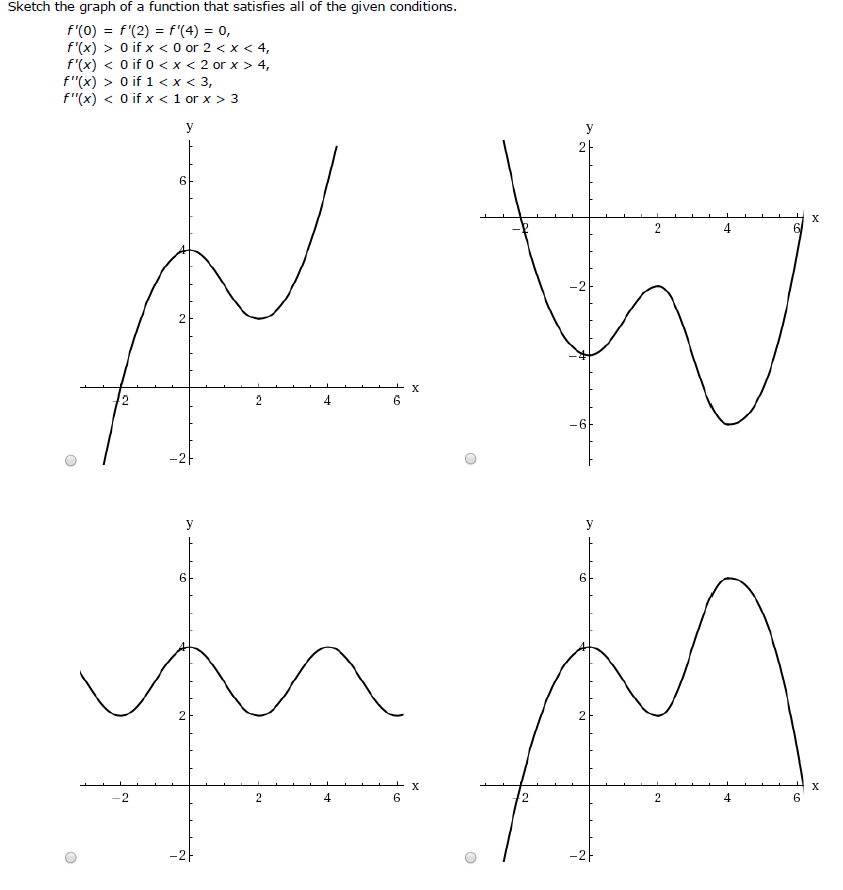



Sketch The Graph Of A Function That Satisfies All Of Chegg Com



Math Scene Equations Iii Lesson 3 Quadratic Equations
Go to your Math tools and select the Graph tool to graph this situation Set the window so that it shows yvalues from 0 to 100 and xvalues from 0 to 10 Then, paste a copy of the graph in the space provided4321 0 1 2 3 44 3 2 1 0 1 2 3 4 The graphs of f(x) = sinx, and y = x,y = x− x3 6, y = x− x3 6 x5 1,y = x− x3 6 x5 1 − x7 5040X is not equal to 0 or 1 Please explain how to get all values of x when f(x) > 0 and f(x) < 0 and explain how to graph
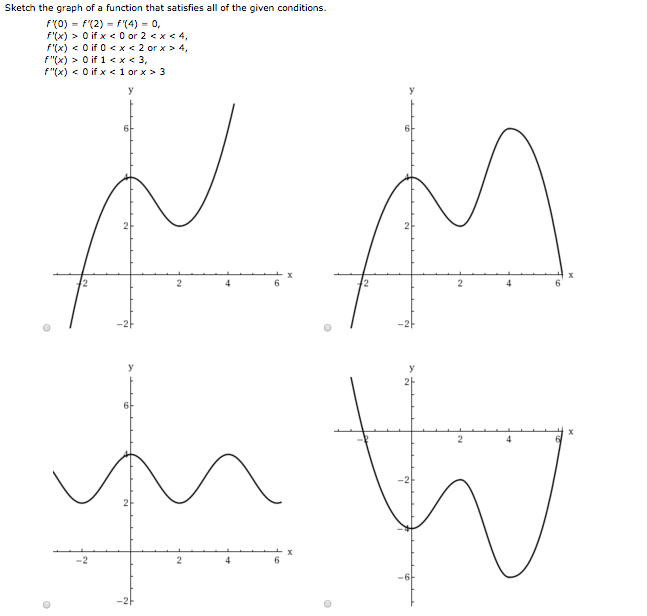



Sketch The Graph Of A Function That Satisfies All Of Chegg Com




Extreme Values Definitions
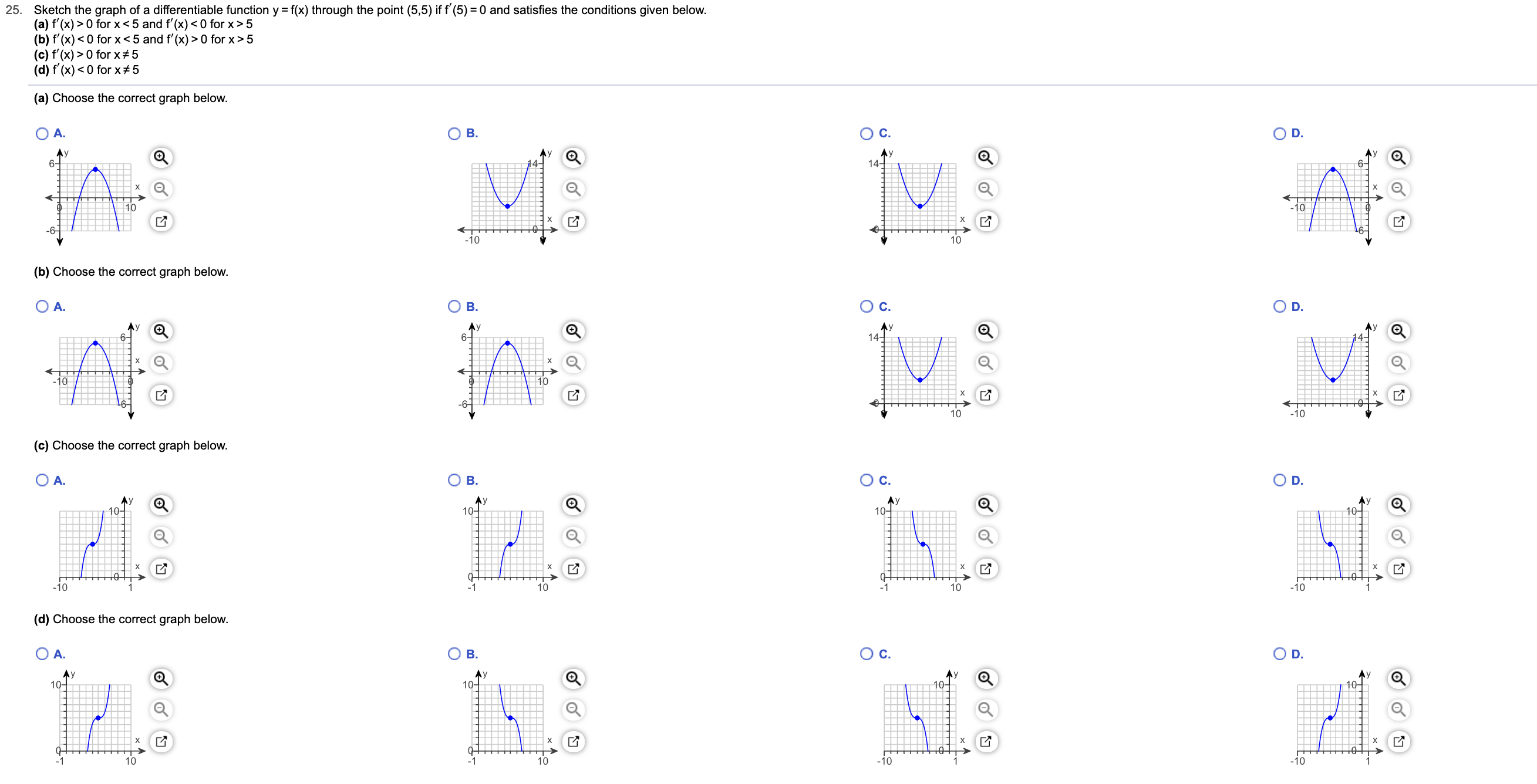
Since the input \(x\) can be any real number the range of \(f\) is all the integers, \(\mathbb{Z}\) The function \(g(x)=xx\) which means it subtracts the whole number part, leaving only the fractional part of the input value \(x\) For integer values of \(x\), \(x=x\) which means that \(g(x)=0\) So the graph of the function looks like thisF(x) = abx where a and b are constants, b > 0 and b ≠ 1 The independent variable is in the exponent Ex f(x) = 2x is an exponential function, but f(x) =Sketch the graph of one function that satisfies ALL of the following conditions (Many correct answers are possible) f(0) = 0 f(4) = 5 So far Sec 26 Limits at Infinity We have seen that the limit of a function at x = a may be ∞ or ∞ But it is also possible to find a limit at infinity




1 Polnts Scalce18 4 3 029 Sketch The Graph Of A Chegg Com



Web Ma Utexas Edu Users Jdanciger Fall11 Hw2 Soln Pdf
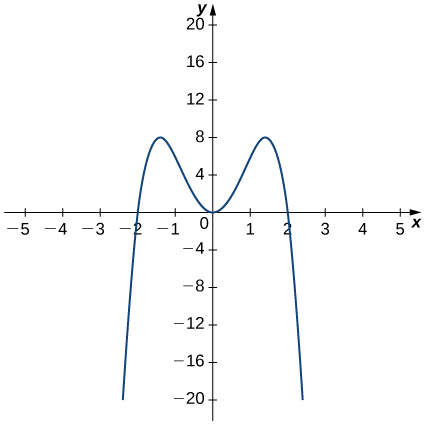
If you were to get the slope of f (x) at the far left it would be increasing 1, 2, 3 and peaking at 4 around x = 75 Then decreasing to 3, 2, 1, 0 Note that those decreasing values 3, 2, 1 are still positive Again its not easy to see just looking at f (x) but the graph of f ' (xTranscribed image text Find all values of x such that f(x) > 0 and all x such that f(x) < 0 and sketch the graph of f 1) F(x) = x^2(x2)(x1)^2(x2) Answer f(x) > 0 if x > 2 f(x) < 0 if x < 2 ;Xaxes y = 0 The range of a function f is the set of values which the function f takes The function f(x,y) = 1 x2 for example takes all values ≥ 1 The graph of f(x,y) is the set {(x,y,f(x,y)) (x,y) ∈ D } The graph of f(x,y) = p x 2y2 on the domain x y2 < 1 is a half sphere Here are more examples
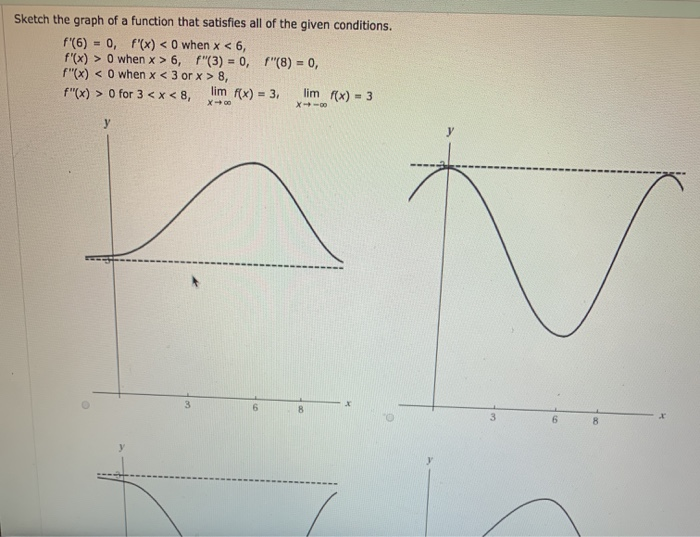



Sketch The Graph Of A Function That Satisfies All Of Chegg Com
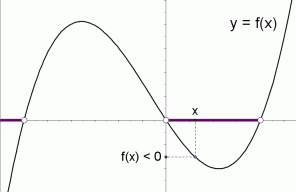



Graphical Interpretation Of Sentences Like F X 0 And F X 0
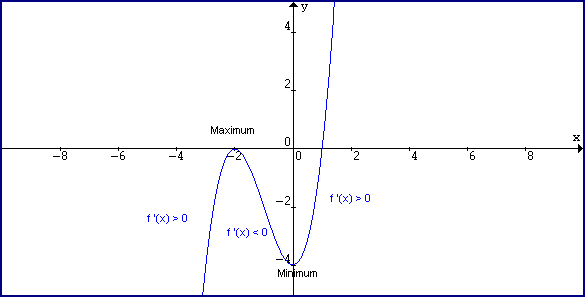
From the graph of f(x), draw a graph of f ' (x) We can see that f starts out with a positive slope (derivative), then has a slope (derivative) of zero, then has a negative slope (derivative) This means the derivative will start out positive, approach 0, and then become negative Be Careful Label your graphs f or f ' appropriately When we're graphing both functions and their derivativesA logarithmic function f(x) = log a (x) , a > 0, a 1, x > 0 (logarithm to the base a of x) is the inverse of the exponential function y = ax Therefore, we have the following properties for this function (as the inverse function) (I) y = log a (x) if and only if a y = x This relationship gives the definition of log a (x f(0) = 1 ≥ 1 x2 1 = f(x) for all real numbers x, we say f has an absolute maximum over ( − ∞, ∞) at x = 0 The absolute maximum is f(0) = 1 It occurs at x = 0, as shown in Figure 412 (b) A function may have both an absolute maximum and an absolute minimum, just one extremum, or neither
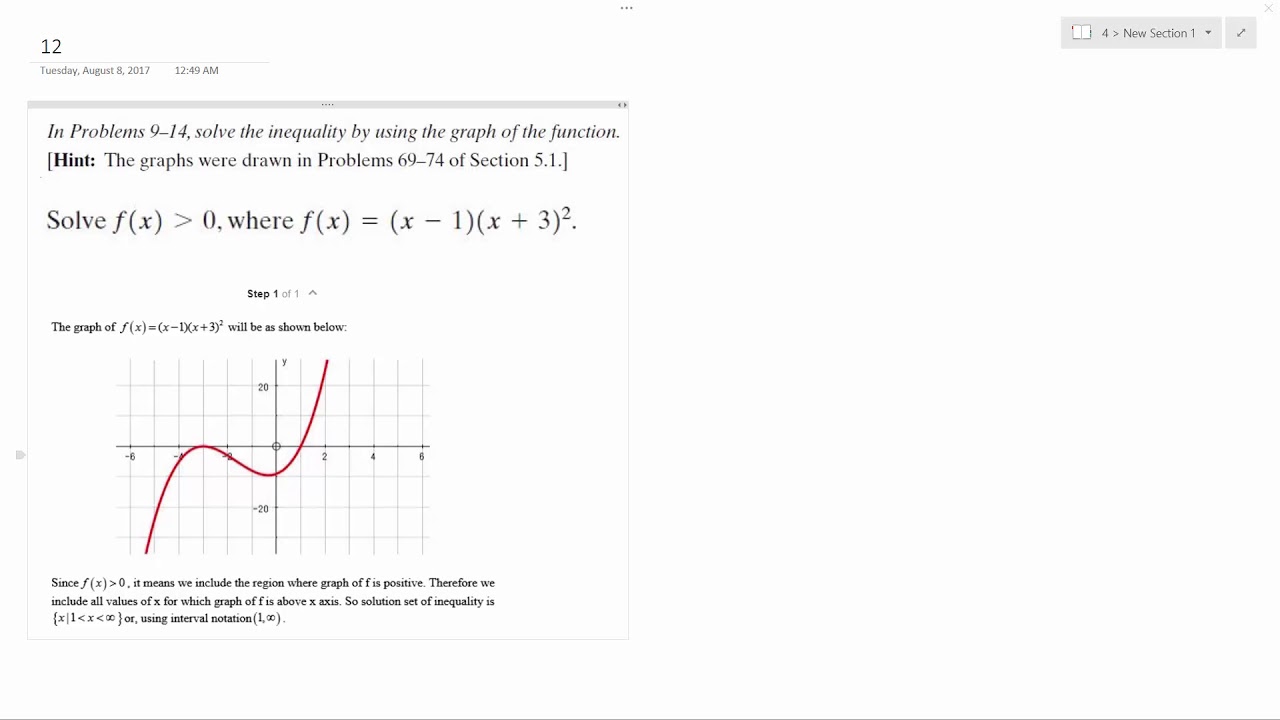



Solve F X Greater Than 0 Where F X X 1 X 3 2 Youtube



Increasing And Decreasing Functions
A function f has an absolute maximum at c if f(c) ≥ f(x) for all x in the domain of f The function value f(c) is the maximum value A function f has an absolute minimum at c if f(c) ≤ f(x) for all x in the domain of f The function value f(c) is the minimum value The absolute maximum and minimum values are called the extreme values of fExplain why Since 4 25 is positiveA) If f'(x) >0 on an interval, then f is increasing on that interval b) If f'(x) 0 on an interval, then f is concave upward on that interval d) If f''(x)



4 5 Derivatives And The Shape Of A Graph Mathematics Libretexts



Secure Media Collegeboard Org Digitalservices Pdf Ap Apcentral Ap13 Calculus Q4 Pdf
0 and as x ?2 (a) Define uniform continuity on R for a function f R → R (b) Suppose that f,g R → R are uniformly continuous on R (i) Prove that f g is uniformly continuous on R (ii) Give an example to show that fg need not be uniformly continuous on R Solution • (a) A function f R → R is uniformly continuous if for every ϵ > 0 there exists δ > 0 such that f(x)−f(y) < ϵ for all x For this equation, The parabola opens upward because a > 0, resulting in a vertex that is a minimum The yintercept of the quadratic function f (x) = x² 3x 4 is (0, c), ie, the point From we get the xintercepts at The axis of symmetry is , ie, The minimum value is The vertex is where or



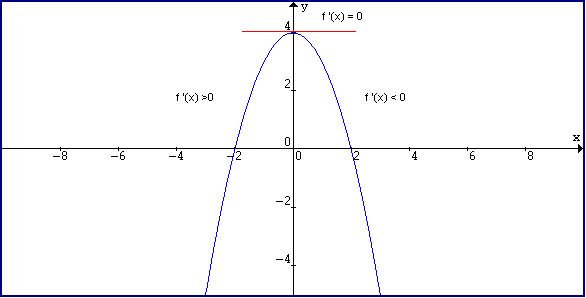
Derivative And Tangent Line



Math Ou Edu Forester 1914f14 Hw8 Pdf
01 Reminder For a function of one variable, f(x), we flnd the local maxima/minima by difierenti ation Maxima/minima occur when f0(x) = 0 † x = a is a maximum if f0(a) = 0 and f00(a) < 0;A point where f00(a) = 0 and f000(a) 6= 0 is called a point of in°ection Geometrically, the equation y = f(x) represents a curve in the twoAlgebra Graph f (x)=x f (x) = x f ( x) = x Find the absolute value vertex In this case, the vertex for y = x y = x is (0,0) ( 0, 0) Tap for more steps To find the x x coordinate of the vertex, set the inside of the absolute value x x equal to 0 0 In this case, x = 0 x = 0 x = 0 x = 0



Http Smacmathapcalculus Weebly Com Uploads 1 9 2 5 Apc Hw 4 6 Key Pdf




Question Video Finding The Solution Set Of A Quadratic Equation Graphically Nagwa
0 f(x) = lim x ?6 Complete the table and use the result to estimate the limit given 0 sin(9 ) lim x x x x01 001 0001 0 0001 001 01 f(x) ?The graph f (x) = ex is given below a 6 pt Sketch f I(x) on the same axes and label three key points on the graph 1 (0,1) b 2 pt State the equation of the function f 1 (x) = 2X1 18 Given the function f (x) a 8 pt Find the inverse function f b 2 pt



3 2 The Derivative As A Function Calculus Volume 1



Cochranmath Analysis Of Curves




Curve Sketching



What Does F 0 Represent On The Graph Of F X Quora



Www Tamdistrict Org Cms Lib Ca Centricity Domain 3 12 Exam Solutions with detailed solutions Pdf
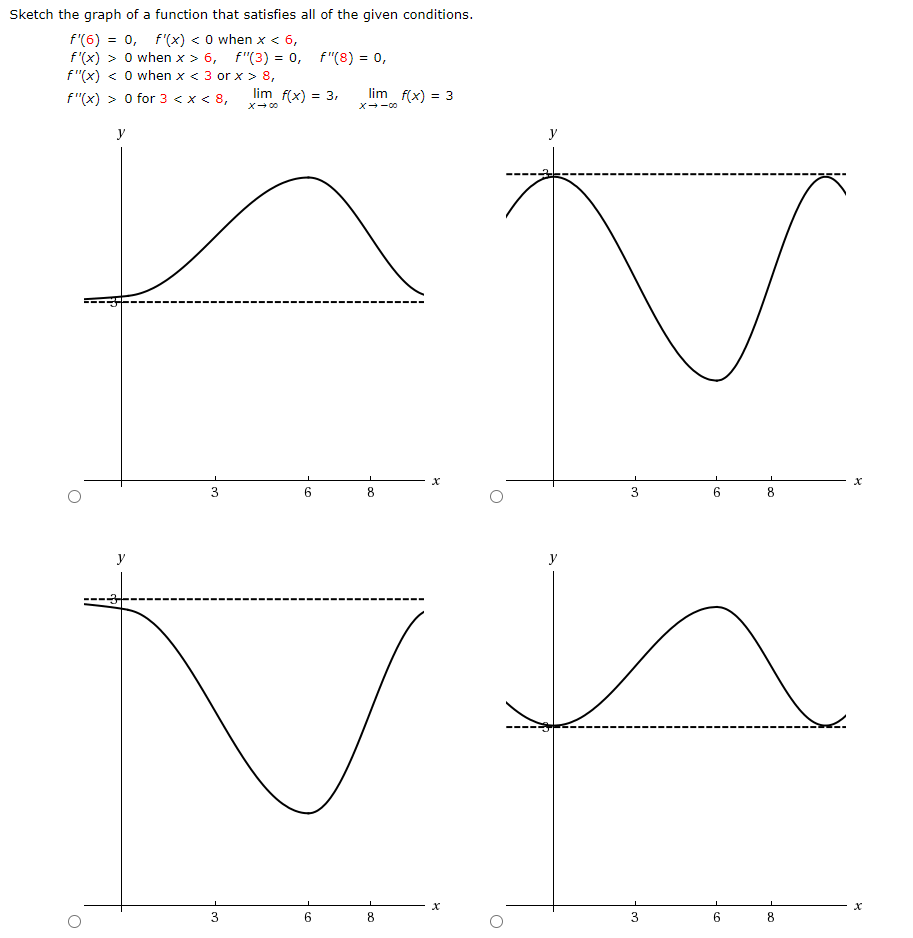



Sketch The Graph Of A Function That Satisfies All Of Chegg Com



Content Newton S Method
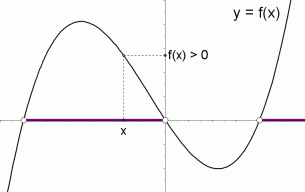



Graphical Interpretation Of Sentences Like F X 0 And F X 0



Solved 5 Details Scalcet8 4 Sketch The Graph Of A Function That Satisfies All Of The Given Conditions F X Gt 0 For All X 1 Vertical Asymp Course Hero




Limits



1



Math Usu Edu Rheal Math1210 Lecture Notes Review For Midterm 2 Concepts Pdf



Calc 1 F X 0 If X 0 What Does This Mean Physics Forums



Math Ou Edu Forester 1914f14 Hw8 Pdf



Curve Sketching
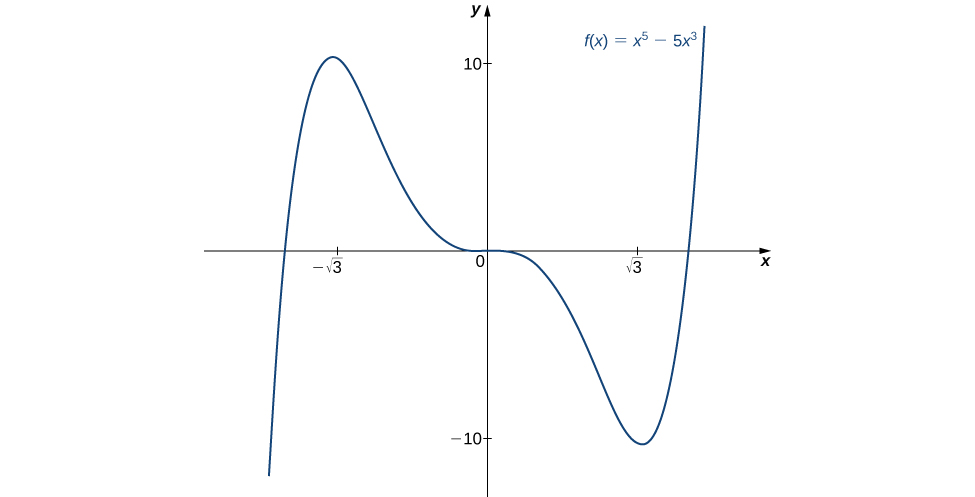



4 5 Derivatives And The Shape Of A Graph Calculus Volume 1




X 2 If 2 X 0 4 X If 2 X 6 Pdf Free Download




14 2 What Values Of X Does F X 0 Youtube



Answered The Graph Of F X Is Shown Below Bartleby



F F F Graphs
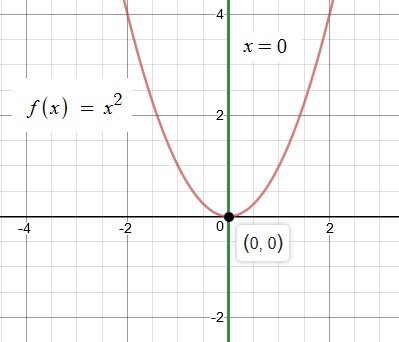



How Is The Graph Of H X X 2 2 Related To The Graph Of F X X 2 Socratic




Help Needed With Calculus Question Wyzant Ask An Expert
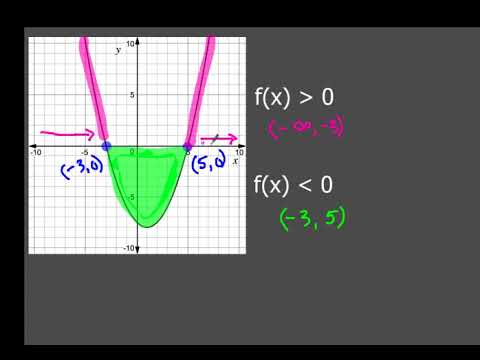



How To Tell Where F X Is Less Than 0 Or Greater Than 0 Youtube




Sketch The Graph Of A Function That Satisfies All Of Chegg Com




Curve Sketching



Www Hoodriver K12 Or Us Cms Lib Or Centricity Domain 230 Ch 5 pt answer key Pdf



What Does F 0 Represent On The Graph Of F X Quora



Www Hoodriver K12 Or Us Cms Lib Or Centricity Domain 230 Ch 5 pt answer key Pdf



Lori Pearman



Solved Sketch The Graph Of Function F That Satisfies The Following Conditions Course Hero




Use The Given Graph Of F X To Determine The Intervals Where F X Greater Than 0 F X Less Than 0 The X Values Where F X 0 And Where F X Is



Http Mathematics Ku Edu Sites Math Drupal Ku Edu Files Files Rajaguru Coursedocuments Sec4 3curvesketching Pdf




4 3 Connecting F And F With The Graph Of F Magic Light Calculus
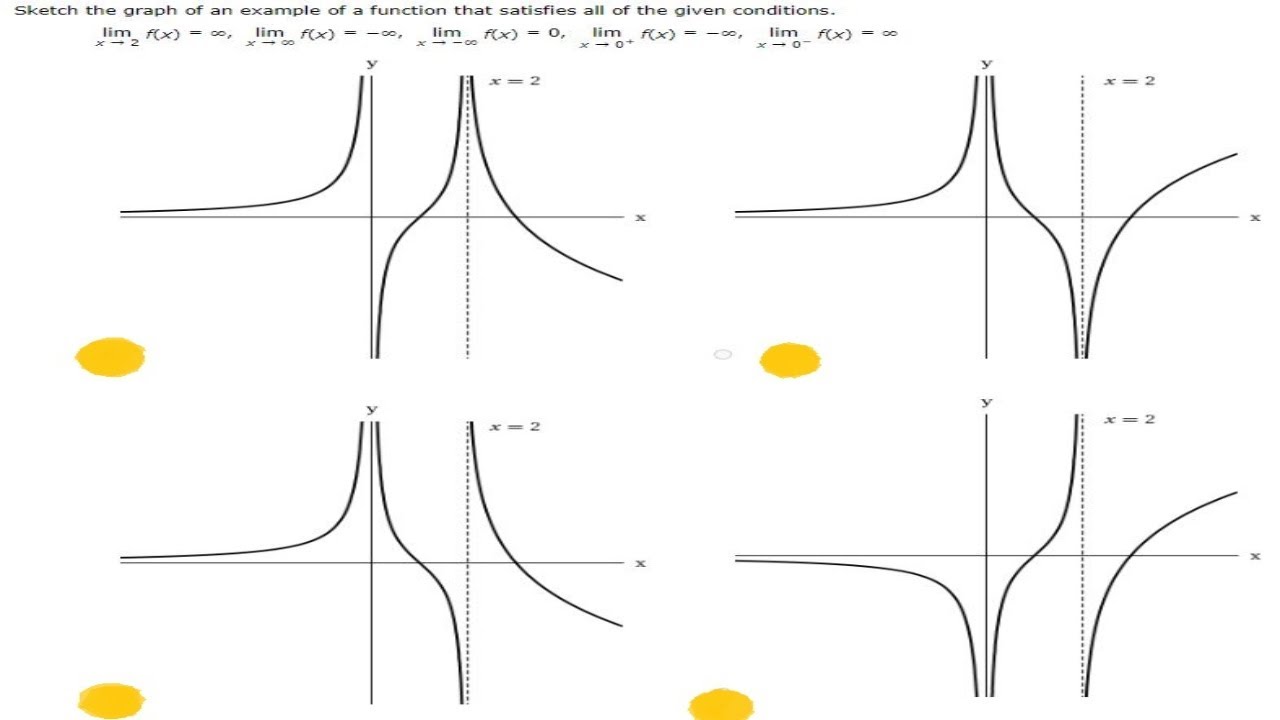



Sketch The Graph Of An Example Of A Function That Satisfies The Given Conditions Limx 2f X Youtube
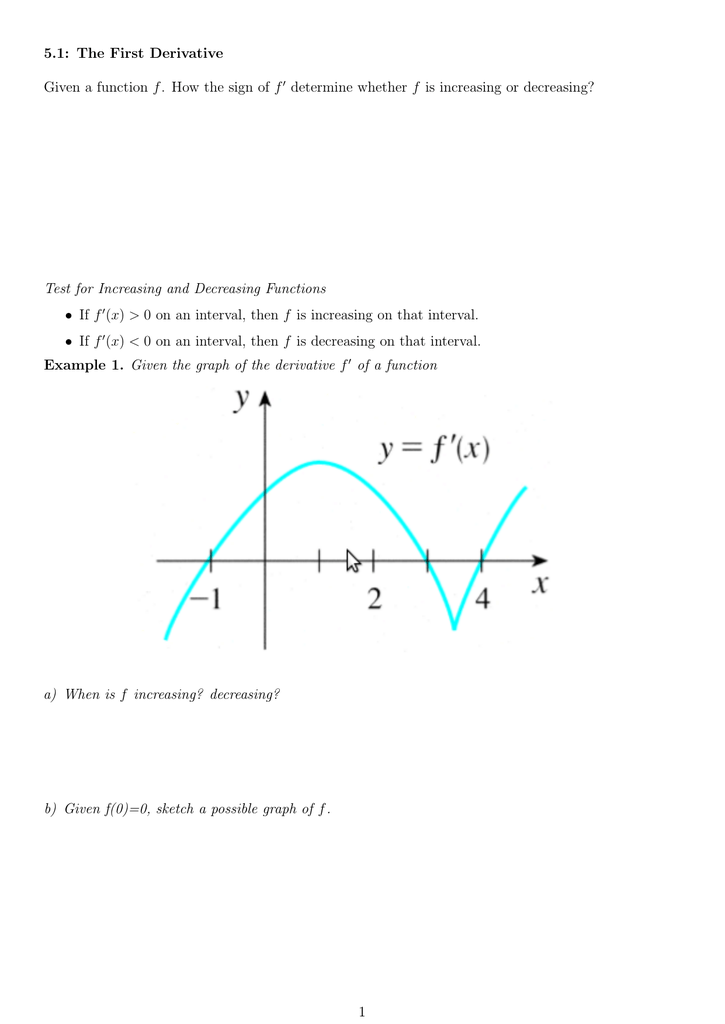



5 1 The First Derivative Determine Whether F Is Increasing Or Decreasing



Math Ou Edu Forester 1914f14 Hw8 Pdf



Sage Calculus Tutorial Differentiability




Graphs Of F X F X F X And X 0 F T Dt For Example 29 5 Download Scientific Diagram



Http Www Math Ntu Edu Tw Cheng Teaching Calculus Ch04 Pdf



Answer In Calculus For Desmond



Http Math Colorado Edu Nita Someexam2practicesol Pdf



Answered Sketch The Graph Of A Differentiable Bartleby



Business Calculus




Ex Determine The Sign Of F X F X And F X Given A Point On A Graph Youtube



Graph Of F X X 3 X 0 X 10 Geogebra



Derivative And Tangent Line




Sketch The Graph Of A Function That Satisfies All Of The Given Conditions F X Is Greater Than 0 For All X Not Equal To One Vertical Asymptote X 1 And F X




Graphing The Basic Functions
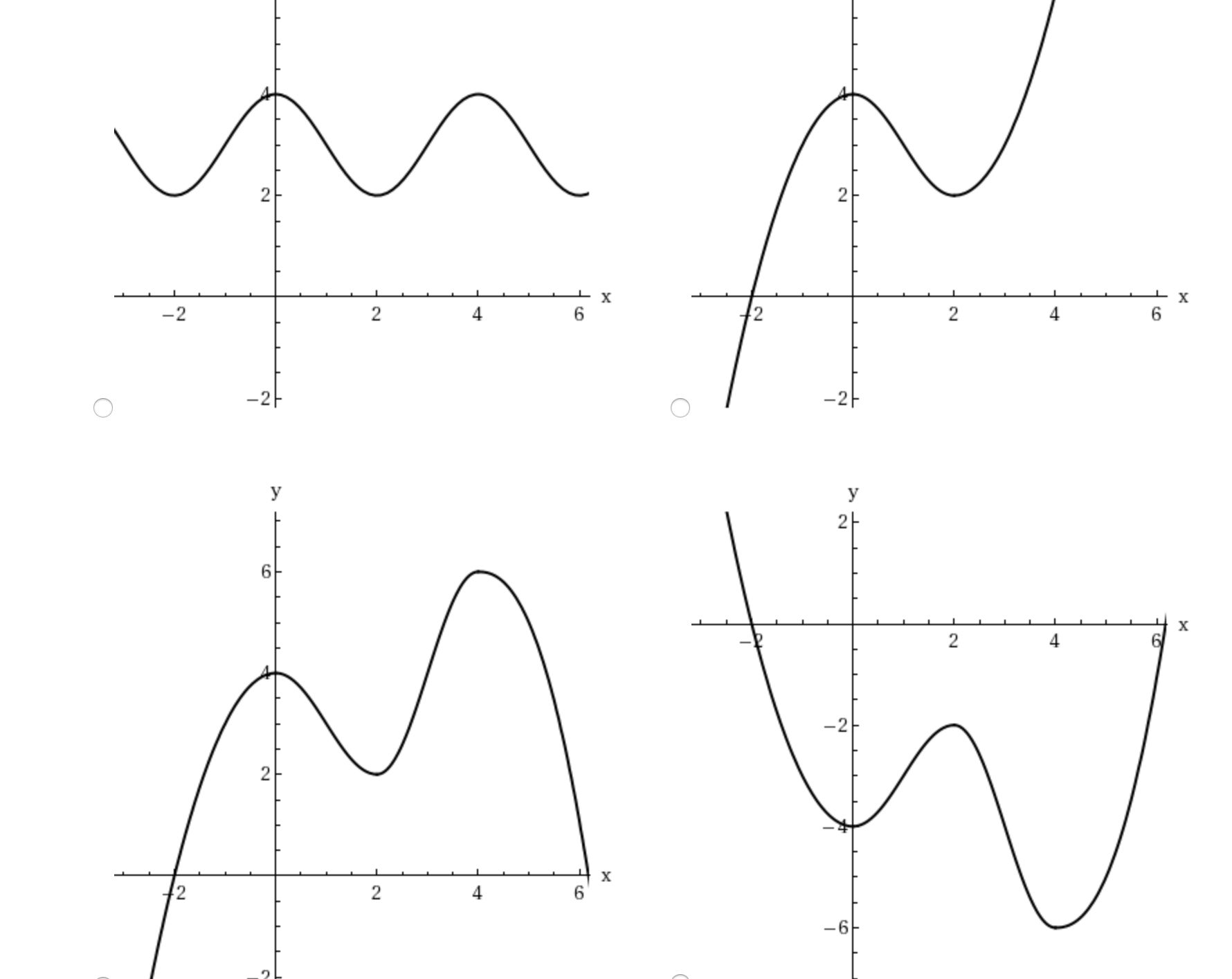



Sketch The Graph Of A Function That Satisfies All Of Chegg Com
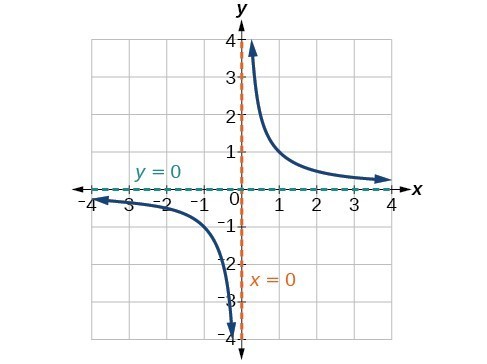



Characteristics Of Rational Functions College Algebra
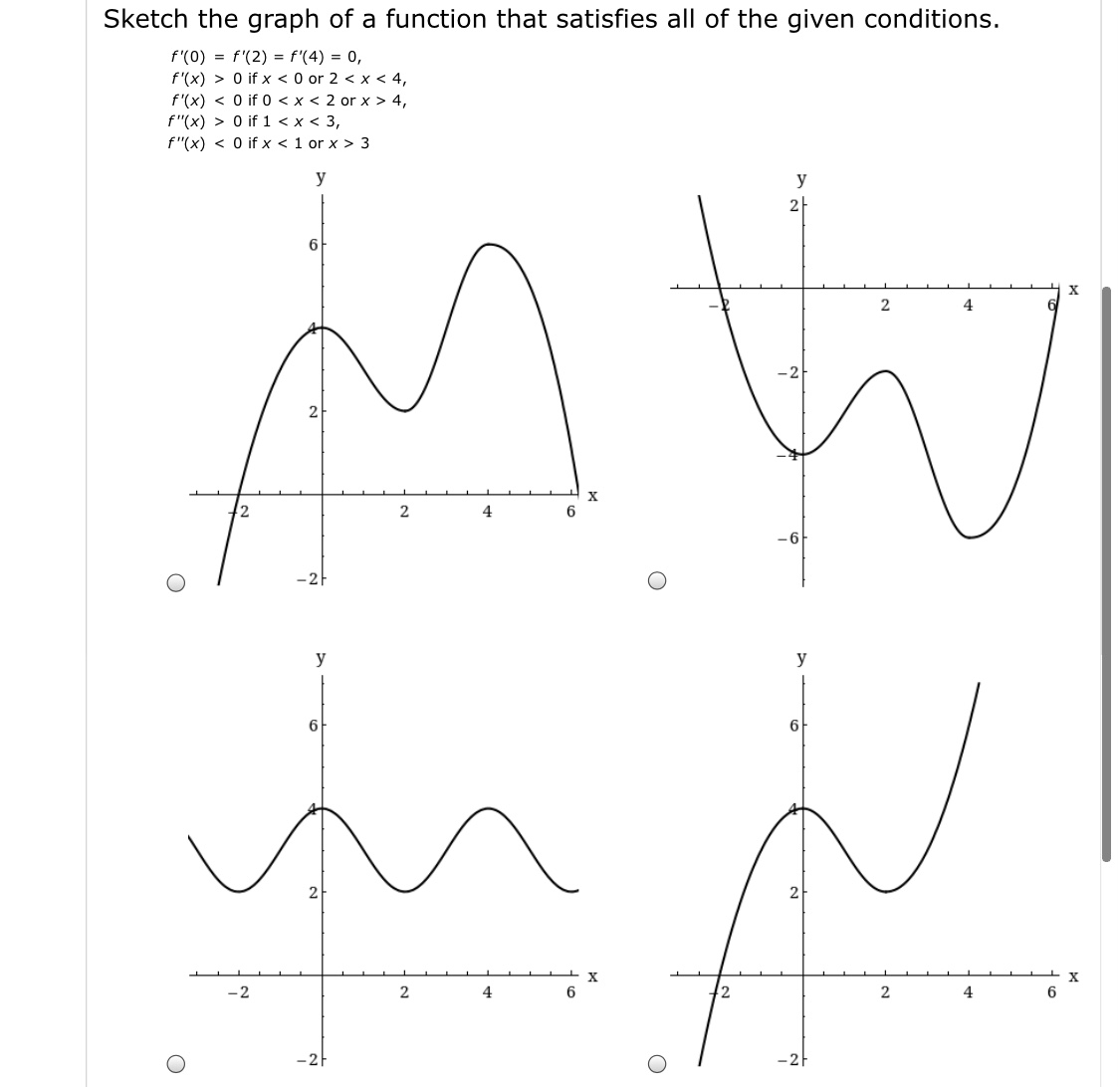



Answered Sketch The Graph Of A Function That Bartleby



What Does F 0 Represent On The Graph Of F X Quora



Http Smacmathapcalculus Weebly Com Uploads 1 9 2 5 Apc Hw Test 5 Extra Practice Key V2 Pdf



Www Tvschools Org Userfiles 281 Classes 4 4 hw Pdf Id



Search Q Interval Notation Tbm Isch



Curve Sketching F X




Sketch The Graph Of A Function That Satisfies The Following Conditions F 2 F 2 0 F X Less Than 0 For X Less Than 2 F X Greater Than 0 If 2 Less



Www Southhadleyschools Org Cms Lib Ma Centricity Domain 11 Ch4sol Pdf



Test 6 Solutions Page 4



Graphing A Function Using The First Derivative Graph Math100 Mirka



Solving Polynomial Inequalities By Graphing
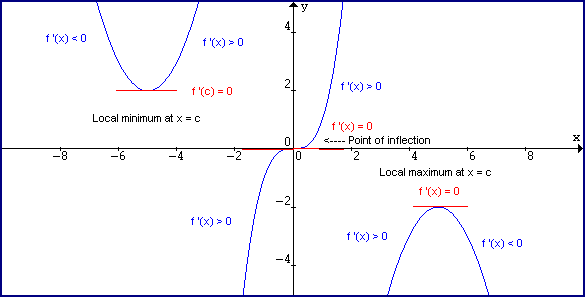



Derivative And Tangent Line



Http Math Colorado Edu Nita Someexam2practicesol Pdf




Match The Conditions F X Less Than 0 And F X Less Than 0 With One Of The Graphs In The Figure Study Com



071maxima Lbz



Calculus Questions With Answers 2



Solution Graph The Piecewise Function Show All Work F X X If X Amp 04 0 And 0 If 0 Lt X Lt 5 And 2x 10 If X Amp 05 5 State Whether The Function Is Continuous If It Is



1



Calculus Questions With Answers 2
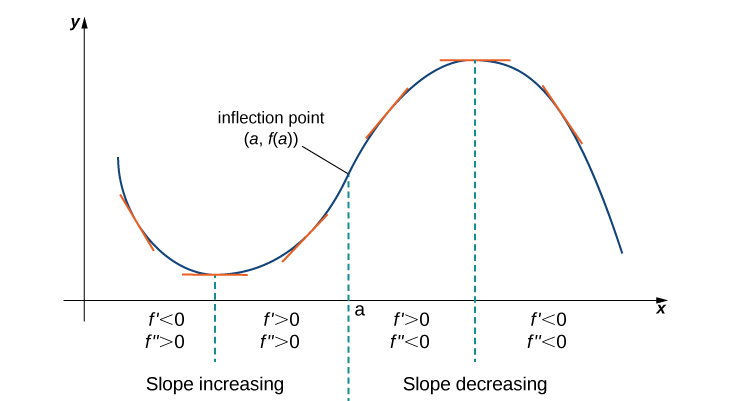



3 5 Derivative Tests Mathematics Libretexts
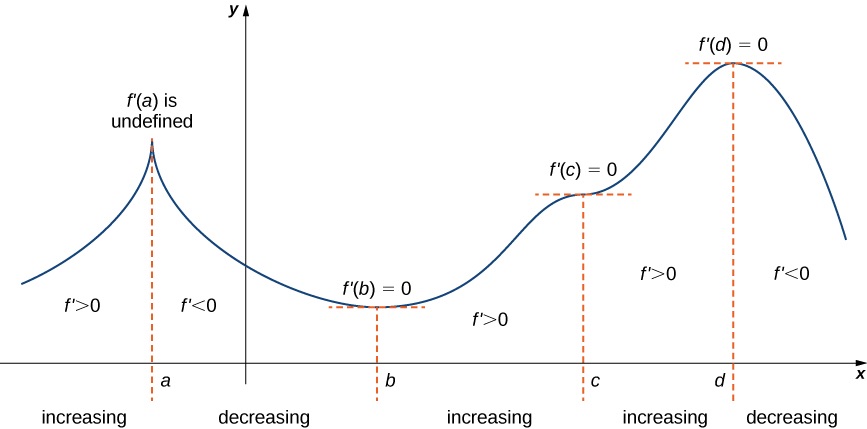



4 5 Derivatives And The Shape Of A Graph Mathematics Libretexts




I Can Sketch The Graph Of F Given The Graph Of F Ppt Download
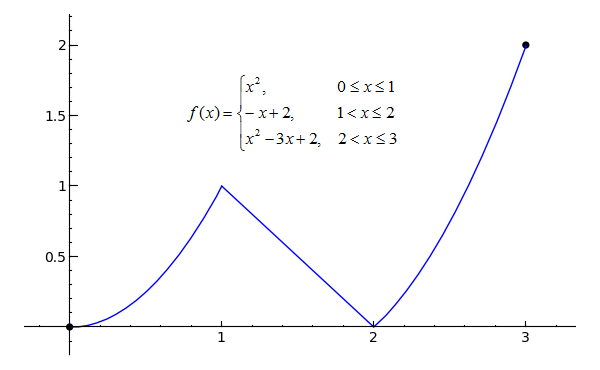



Sage Calculus Tutorial Continuity



Solution If F X X X 1 X 4 Use Interval Notation To Give All Values Of X Where F X Gt 0



0 件のコメント:
コメントを投稿